2024年度　群馬県公立高校入試問題過去問【数学】解説

平均52.8点（前年比；－6.7点）

問題はコチラ→ＰＤＦファイル

大問１（大問集合）

（１）①
７＋（－２）
＝７－２
＝５

②
（３ｘ＋７）－（ｘ－１）
＝３ｘ＋７－ｘ＋１
＝２ｘ＋８

③
（３ａ²ｂ－２ａｂ）÷ａｂ　←分配法則
＝３ａ²ｂ÷ａｂ－２ａｂ÷ａｂ
＝３ａ－２

（２）
ｘ²－５ｘ－24
＝（ｘ－８）（ｘ＋３）

（３）
ア：0.1＝√（0.1）²＝√0.01×
イ：（√10）²＝10〇
ウ：３の平方根＝２乗すると３になる数→±√３×
エ：３√11＝√99、10＝√100
√99＜√100だから、３√11＜10〇
イ・エ

（４）
底面積×２＋側面積
＝５×５×π×２＋５×２×π×６
＝110πｃｍ²

（５）
ｘ²＋５ｘ＋５＝０
解の公式を適用、ｘ＝（－５±√５）/２

（６）
∠ＡＣＢ＝180－64×２＝52°

（７）
三平方の定理より、ＡＣ²＝41²－40²
＝（41＋40）（41－40）＝81
ＡＣ＞０だから、ＡＣ＝９ｃｍ

（８）
全体は、６×６＝36通り
条件が変わる大の出目で場合分け。
●大が３以下【和】
（大、小）＝（１、４）（２、３）（３、２）の３通り。
●大が４以上【積】
（大、小）＝（４、５）（５、１～６）（６、５）８通り。
計11通りだから、確率は11/36。

（９）
『ｙはｘの２乗に比例する』→ｙ＝ａｘ²
（ｘ、ｙ）＝（10、10）を代入、10＝100ａ
ａ＝１/10

ｙ＝１/10ｘ²にｘ＝30を代入。
ｙ＝１/10×900＝90ｍ

大問２（方程式）

（１）
左はａｇ、右は２ｂ＋50ｇ。
右の方が重い（値が大きい）ので、ａ＜２ｂ＋50

（２）
答案では求める過程を書く。
〇１個をｘｇ、☆１個をｙｇとする。
３ｘ＝２ｙ　…①
２ｘ＋80＝３ｙ　…②

①を３/２倍すると、９/２ｘ＝３ｙ
これを②に代入。２ｘ＋80＝９/２ｘ
５/２ｘ＝80
ｘ＝32
①に代入、ｙ＝32×３÷２＝48
丸型１個…32ｇ、星型１個…48ｇ

＠別解＠

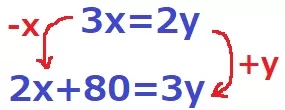
ｘを１個減らして、ｙを１個増やすと＋80で等しくなる→80の差が生まれた。
１回の交換で80差ということは、ｘ＋ｙ＝80がいえる。
ｘ＝80－ｙを下の式に代入して、
２（80－ｙ）＋80＝３ｙ
５ｙ＝240
ｙ＝48と求めることもできる。

大問３（平面図形）

（１）

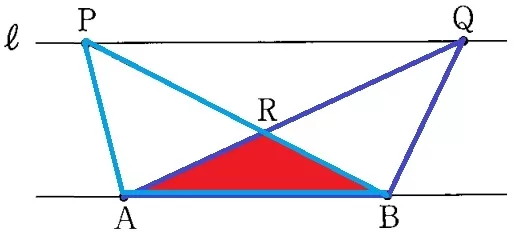
△ＰＡＢと△ＱＡＢについて、共通辺のＡＢを底辺と考えると、
ℓ//ＡＢより高さが等しいから、△ＰＡＢ＝△ＱＡＢ
Ｘ…ＡＢ、Ｙ…高さが等しい
＠
（証明の続きを述べる）
２つの三角形から共通部分の△ＲＡＢをひく。
△ＰＡＲ＝△ＰＡＢ－△ＲＡＢ
△ＱＢＲ＝△ＱＡＢ－△ＲＡＢ
したがって、△ＰＡＲ＝△ＱＢＲ

（２）①②

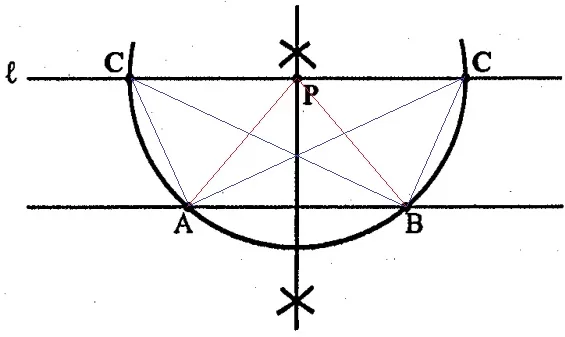
『ＰＡ＝ＰＢ』→ＰはＡとＢから等距離にある。
ＡＢの垂直二等分線とℓとの交点がＰ。
『∠ＡＣＢ＝１/２∠ＡＰＢ』→円周角の定理を思い浮かべる。
弧ＡＢに対する中心角ＡＰＢと円周角ＡＣＢの関係から条件に適合する。
Ｐを中心とする円を描き、ℓとの２つの交点がＣ。

大問４（データの活用）

（１）

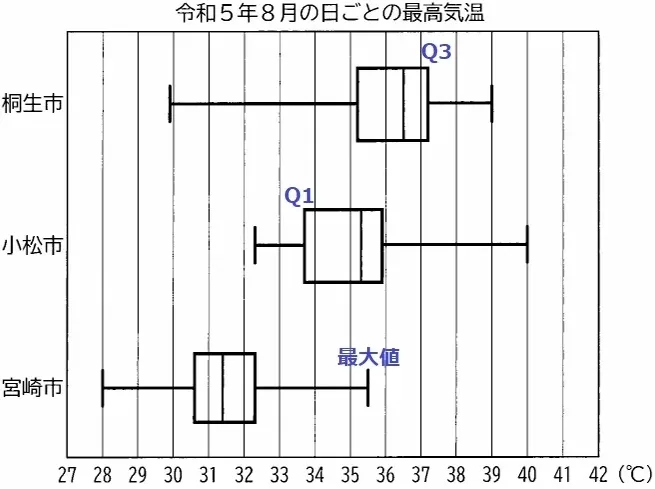
小さい順に、小松市の第１四分位数（Q1）＜宮崎市の最大値＜桐生市の第３四分位数（Q3）
イ・ウ・ア

（２）

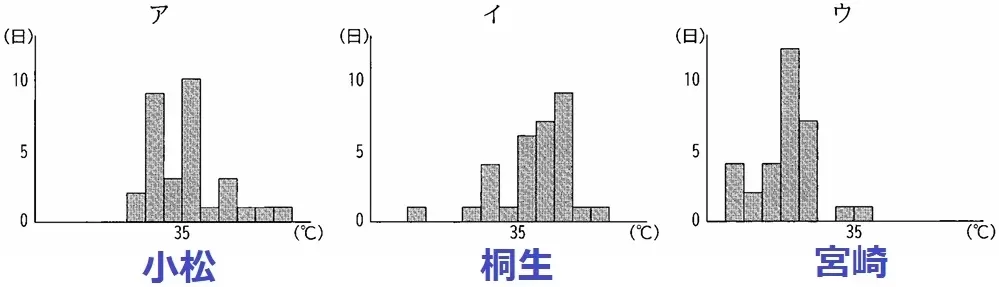
判断しやすい最小値・最大値から判断する。
最小値が最も小さいウが宮崎市、最大値が最も大きい小松市がア。
残りのイが桐生市。
イ

（３）
ア：範囲（レンジ）＝最大値－最小値。範囲が大きいのは桐生市。〇
イ：四分位範囲＝Q3－Q1。箱の長さが最も長い小松市。×
ウ：小松市のQ3は36℃→小松市の全体の１/４以上が36℃以上。
対して、桐生市の中央値は36℃を超えている→過半数が36℃以上だから桐生市の方が多い。×
エ：31日の中央値は16番目の値。
桐生市の16番目は宮崎市の最大値より大きい→桐生＞宮崎は少なくとも16日ある。〇
ア・エ

大問５（方程式２）

（１）①

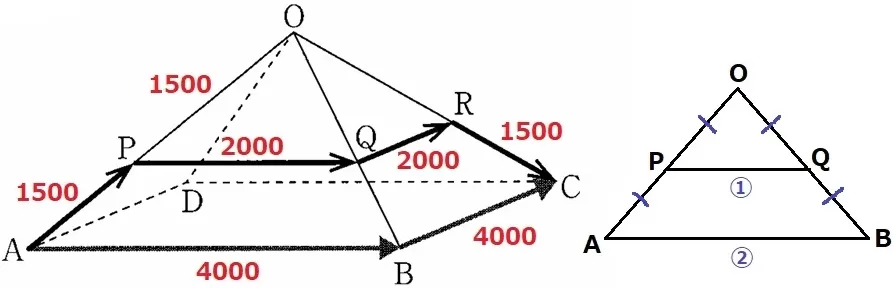
ＰとＱはそれぞれＯＡとＯＢの中点である。
中点連結定理から、ＰＱ＝4000÷２＝2000ｍ
Ｑが真ん中の点。全体の距離は、（1500＋2000）×２＝7000ｍ

②

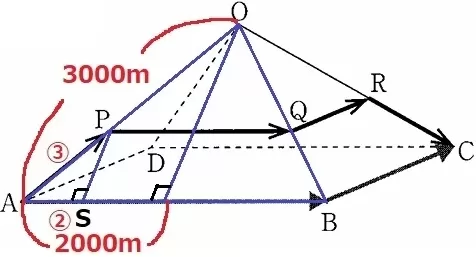
Ｏから垂線をひくと、辺の比が3000：2000＝３：２の直角三角形がある。
Ｐから垂線をおろし、足をＳとする。直角三角形の相似よりＡＰ：ＡＳ＝③：②

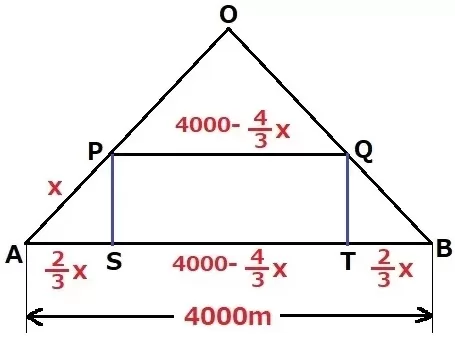
ＡＰ＝ｘだから、ＡＳ＝２/３ｘ
Ｑから垂線をひき、足をＴとする。対称性からＢＴ＝２/３ｘ
ＰＱ＝ＳＴ＝4000－２/３ｘ×２＝4000－４/３ｘ
Ａ→Ｐ→Ｑの距離は、ｘ＋（4000－４/３ｘ）＝－１/３ｘ＋4000
Ｑは真ん中なので、ｙ＝２（－１/３ｘ＋4000）＝－２/３ｘ＋8000

③
Ａ→Ｂ→Ｃの90％…4000×２×90％＝7200ｍ
Ａ→Ｐ→Ｑ→Ｒ→Ｃの距離はｙだから、前問の式にｙ＝7200を代入すればいい。
7200＝－２/３ｘ＋8000
２/３ｘ＝8000
ｘ＝1200
1200ｍ

（２）
展開すると、Ａ→Ｂ→ＣとＰ→Ｑ→Ｒは直線ではない。
上から見た図で確認する。

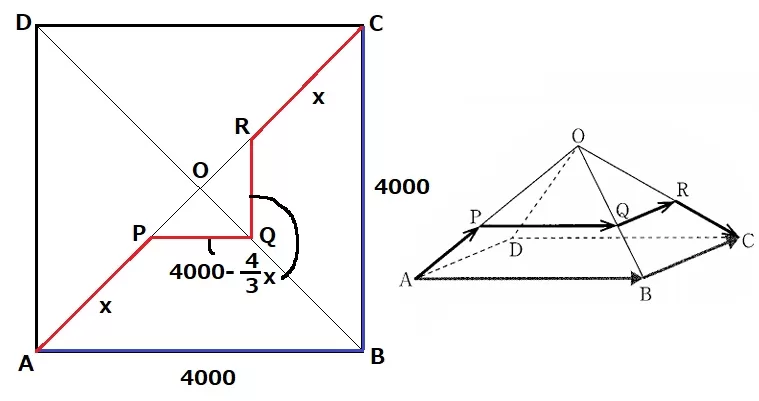
（１）②より、ＰＱ＋ＱＲ＝（4000－４/３ｘ）×２＝8000－８/３ｘ
赤線ルートの時間が青線ルートの時間の90％になる。
時間で等式を立てるとして、速さは比しかわかっていない。
速さの比は、上り（ＡＰ）：平地：下り（ＲＣ）＝0.6：１：1.5＝６：10：15

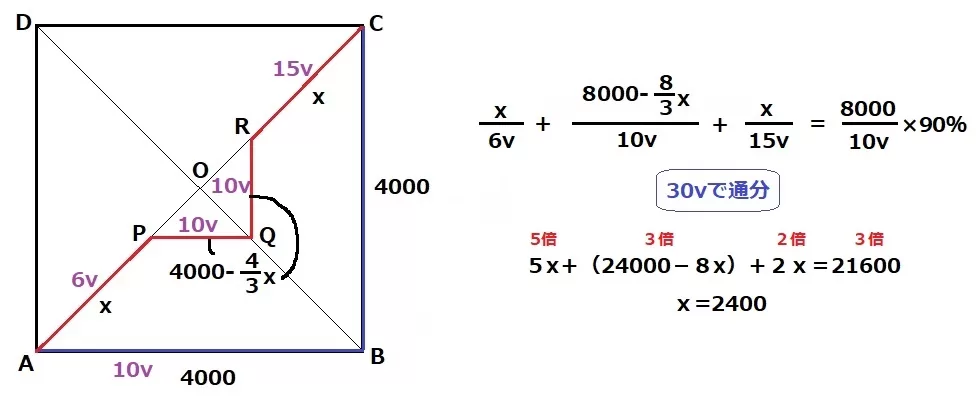
速さの比例定数をｖとする。（ｖ；速度velocityの頭文字で高校物理で扱う）
上り（ＡＰ）：平地：下り（ＲＣ）＝：６ｖ：10ｖ：15ｖ
距離÷速さでそれぞれの区間の時間を表し、その合計で方程式を立てる。

ｘ/６ｖ＋（8000－８/３ｘ）/10ｖ＋ｘ/15ｖ＝8000/10ｖ×90％　←×30ｖ
５ｘ＋３（8000－８/３ｘ）＋２ｘ＝7200×３
５ｘ＋（24000－８ｘ）＋２ｘ＝21600
ｘ＝2400
2400ｍ

＠余談＠
こういう問題を見ると算数の範囲で攻略できないかと追究したくなり、
あれこれ試行錯誤した結果、見つけました。興味のある方はご覧ください。

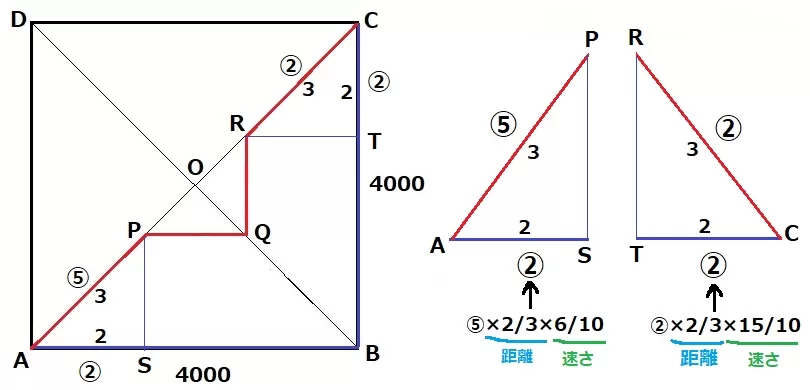
ＡＰとＲＣは距離一定。
速さの比が６：15＝２：５なので、時間の比は逆比でＡＰ：ＲＣ＝⑤：②です。

ＡとＲから垂線をおろし、足をＳ・ＴとしてＡＳの時間を求めます。
距離はＡＰの２/３倍、ＡＳの方が速いので、時間は逆比でＡＰの６/10倍です。
ＡＳの時間…⑤×２/３×６/10＝②
ＡＳとＣＴは距離一定かつ速さ一定ですから、ＣＴの時間も②。
（計算で求めると、②×２/３×15/10＝②）

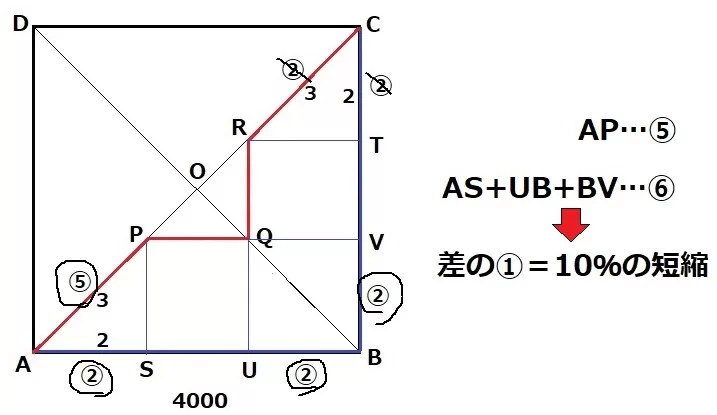
Ｑから垂線をひき、それぞれをＵ・Ｖとします。
赤線ルートと青線ルートの相違点に着目すると、⑤（ＡＰ）←→⑥（ＡＳ＋ＵＢ＋ＢＶ）
差の①が短縮分の10％に相当する。
青線ルートの時間を⑩とすると、赤線ルートの時間は⑨です。

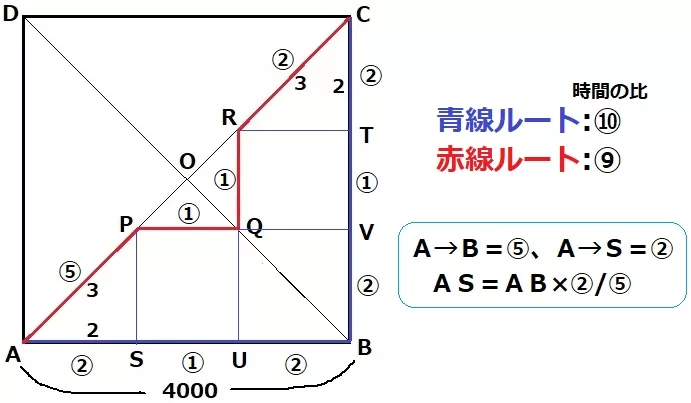
Ａ→Ｂまでが⑩÷２＝⑤、Ａ→Ｓまでが②の時間で速さは一定ですから、
距離の比はＡＳ：ＡＢ＝②：⑤
ＡＳ＝4000×②/⑤＝1600ｍ
ＡＰ：ＡＳ＝３：２なので、ＡＰ＝1600×３/２＝2400ｍ