平均50.7点(前年比;-4.5点)
問題はこちら→東進ハイスクールさん(解答)
出題範囲の除外は円周角と中心角、三平方の定理、資料の活用。
2021年大阪B問題、2021年大阪C問題の解説は別ページ。
大問1(計算)
(1) 89.7%
10-2×8
=10-16
=-6
(2) 72.3%
-12÷(-6/7)
=-12×(-7/6)
=14
(3) 89.7%
52+(-21)
=25-21
=4
(4) 63.2%
6x-3-4(x+1)
=6x-3-4x-4
=2x-7
(5) 67.1%
5x×(-x2)
=-5x3
(6) 58.1%
√7+√28
=√7+2√7
=3√7
大問2(小問集合)
(1) 68.4%
-a+8
=-(-3)+8
=3+8
=11
(2) 50.3%
時間=道のり÷速さ
am÷分速70m=a/70分
ウ
(3) 43.9%
整数の分数で表せる数を有理数、整数の分数で表せない数を無理数という。
ア:1/3〇
ウ:0.2=2/10=1/5〇
エ:√9=3=3/1〇
イ:√2=1.41421356…(一夜一夜に人見頃)
不規則な数字が無限につづく数は、分数で表せない無理数。
イ
@循環小数@
無限に続く小数(無限小数)であっても、
数字の並びが規則的な循環小数は有理数である点に注意!
例えば、0.123123123…を分数に表すと、
1000x=123.123123123…
-) x= 0.123123123…
999x=123
x=123/999=41/333(←有理数!)
(4) 74.2%
x:12=3:2
外項と内項の積は等しい。
2x=12×3
x=18
(5) 57.0%
5x+2y=-5
+)3x-2y=13
8x =8
x=1
上の式にx=1を代入。
5×1+2y=-5
2y=-10
y=-5
x=1、y=-5
(6) 46.9%
x2-4x-21
=(x+3)(x-7)=0
x=-3、7
(7) 20.9%!
55回以上の人数は、20×30%=20×30/100=6人
1+y=6
y=5
x=20-(2+4+5+1)=8人
xの値…8、yの値…5
(8) 35.5%
2枚を取り出す→5×3=15通り
和が4の倍数となる組み合わせを調べる。
(A、B)=(1、3)(3、1)(3、5)(5、3)
最大で5+5=10だから、12は作れない。
計4通り。確率は4/15
(9) 28.4%!
y=ax2に(x、y)=(-4、3)を代入。
3=(-4)2a
a=3/16
(10) 32.9%!

『△DBEは△ABCを点Bを回転の中心として反時計回りに100°回転移動したもの』
辺DBは辺ABに対応する。
∠ABD=100°
正三角形の内角は60°だから、∠ABE=100-60=40°
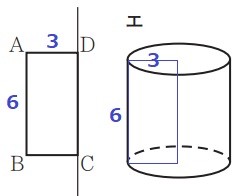
② 29.0%!
3×3×π×6=54πcm3
大問3(一次関数)
(1)ア…81.3%、イ…67.7%

間の数が+25。
ア=10+25×(4-1)=85
イ=10+25×(9-1)=210
ア…85、イ…210
(2) 36.8%
25ずつ増えていくので、傾きは25。
y=25x+bに(x、y)=(1、10)を代入する。
10=25×1+b
b=-15
y=25x-15
(3) 54.2%
先ほどの式にy=560を代入。
560=25x-15
x=23
大問4(平面図形)
(1) 17.2%!
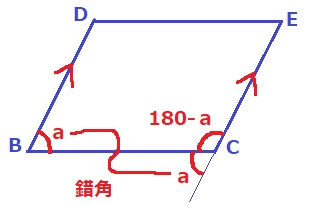
∠DBC=a°を錯角で移動。
∠BCE=180-a°
*平行四辺形の隣り合う内角の和は180°である。
(2)a…71.0%、b…63.9%、c…59.4%
△ABC∽△CFDの証明。
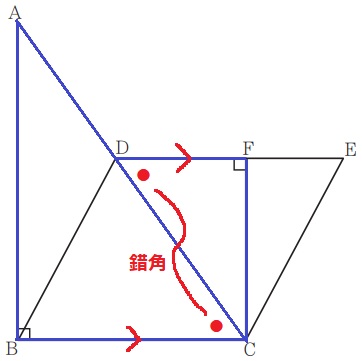
∠ABC=∠CFD=90°
DE//BCより、錯角で∠ACB=∠CDF
2角が等しいので∽
a…CFD、b…CDF、c…ウ
(3) 7.9%!!
解答では求め方も記述する。
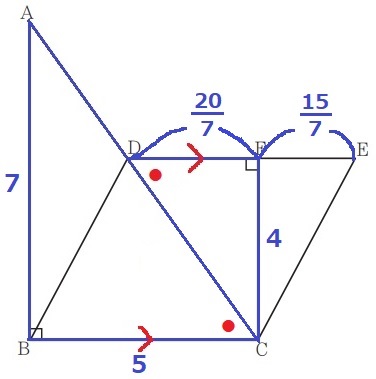
高さFCがわかっているので、底辺FEの長さが知りたい。
前問の△ABC∽△CFDより、BC:FD=AB:CF=7:4
DF=5×4/7=20/7cm
平行四辺形BCEDの対辺は等しく、DE=BC=5cm
FE=5-20/7=15/7cm
△FCEの面積は、15/7×4÷2=30/7cm2
●講評●
大問1
全問死守したい。
大問2
(2)中1で習う文字式。
(3)有理数、無理数の定義は分数で表せるか否か。
(7)先にyを求めてからx。%の計算は出来るように!
(9)難しくない。
(10)どこが100°になるか。どの辺がどこに移動するか。
大問3
(3)の方が正答率が高い。
(3)を解いて(2)に戻っても良い。
大問4
(3)何の情報が知りたいか。答えから逆算して解法を探る。
△FCEの面積⇒FEの長さ⇒DFの長さ⇒前問の△ABC∽△CFD利用



コメント