平均60.2点
問題はコチラ→ＰＤＦファイル
出題範囲の除外は円周角と中心角、三平方の定理、資料の活用。
2021年度Ａ問題、Ｃ問題の解説はコチラから。
大問１（小問集合）
（１） 96.4％
２×（－３）2－22
＝２×９－22
＝18－22＝－４
（２） 93.0％
４（ｘ－ｙ）＋５（２ｘ＋ｙ）
＝４ｘ－４ｙ＋10ｘ＋５ｙ
＝14ｘ＋ｙ
（３） 90.5％
18ｂ×（－ａ2）÷３ａｂ
＝－６ａ
（４） 83.0％
ｘ（ｘ＋７）－（ｘ＋４）（ｘ－４）
＝ｘ2＋７ｘ－ｘ2＋16
＝７ｘ＋16
（５） 79.5％
（２－√５）2
＝４－２√５＋５
＝９－４√５
（６） 83.9％
ｎ角形の内角の和は180（ｎ－２）°
180×（７－２）＝900°
（７） 94.5％
ａ＝１、ｂ＝－１を代入して試す。
エ：ａ－ｂ＝１－（－１）＝２が最も大きい。
エ
（８） 61.4％
最頻値（モード）を含む階級は26～28回の４人。
その相対度数は、４÷12＝0.33…≒0.33
（９） 54.8％
５枚から２枚を取り出す→5Ｃ2＝10通り
ａ/２の値が奇数となる組み合わせを探す。
４は素因数２を２つ含むので、ａ/２の値は偶数となる。
→４は出せない。
６と（３・５・７）の３通り。
確率は３/10。
（10） 19.8％！
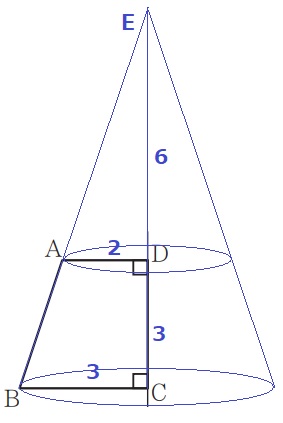
回転体は円錐台（プリン型）になる。
円錐の頂点をＥとする。
ＥＤ：ＥＣ＝ＡＤ：ＢＣ＝２：３
ＥＤ＝２×３＝６ｃｍ
上の円錐の体積比は、２×２×２＝【８】
全体の円錐の体積比は、３×３×３＝【27】
下の円錐台の体積比は、【27】－【８】＝【19】
したがって、円錐台の体積は３×３×π×９÷３×19/27＝19πｃｍ3
大問２（関数）
（１）①ア…94.5％、イ…90.0％
25ずつ増えている。
ア＝10＋25×（４－１）＝85
イ＝10＋25×（９－１）＝210
ア…85、イ…210
② 85.5％
25ずつ増えるので傾きは25。
ｙ＝25ｘ＋ｂに（ｘ、ｙ）＝（１、10）を代入。
10＝25×１＋ｂ
ｂ＝－15
ｙ＝25ｘ－15
③ 81.8％
先ほどの式にｙ＝560を代入。
560＝25ｘ－15
ｘ＝23
（２） 28.9％！
問題文がやけに長いが、ようは左の10ｃｍを変えないまま、
28本の場合と全長を同じくして31本を等間隔で植えるとき、その間隔の距離を求める。
ポイントは間の数でカウントすること！
28本の間（25ｃｍ）の数は27ヶ所ある。31本の間の数は30ヶ所。
25×27＝ａ×30
ａ＝25×27÷30＝45/２ｃｍ
大問３（関数２）
（１） 72.6％
ｙ＝－１/８ｘ2において。
ｘ＝０のとき、最小値ｙ＝０
ｘ＝－７のとき、最大値ｙ＝49/８
０≦ｙ≦49/８
①ア…０、イ…49/８
② 86.3％
ｙ＝－27/ｘにｘ＝－３を代入
ｙ＝－27÷－３＝９
③ 55.2％
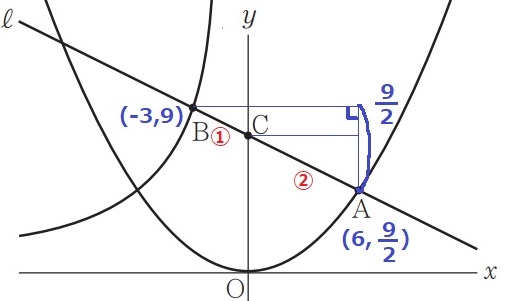
前問より、Ｂ（－３、９）
ｙ＝１/８ｘ2にｘ＝６を代入→Ａ（６、９/２）
ＡとＢのｙ座標の差は、９－９/２＝９/２
ＢＣ：ＣＡ＝３：６＝①：②
Ｃのｙ座標は、９/２＋９/２×②/③＝15/２
（２） 23.2％！
答案では求め方も記述する。
Ｄ（４、２）Ｅ（ｔ、１/８ｔ2）
ＦＥ＝ｔ－４
ＦＤ＝（ｔ－４）＋８＝ｔ＋４
ＤとＥのｙ座標の差で等式を立てる。
１/８ｔ2－２＝ｔ＋４
ｔ2－16＝８ｔ＋32
ｔ2－８ｔ－48
＝（ｔ－12）（ｔ＋４）＝０
ｔ＞４ゆえ、ｔ＝12
大問４（図形）
（１） 34.3％
△ＡＢＦ≡△ＣＤＧの証明。
∠ＡＦＢ＝∠ＣＧＤ＝90°
平行四辺形ＡＢＣＤの対辺は等しい→ＡＢ＝ＣＤ
ＡＢ//ＤＣの同位角と二等辺三角形ＥＤＣの底角をつなげて、
∠ＡＢＦ＝∠ＣＤＧ
斜辺と１つの鋭角が等しい直角三角形ゆえ、△ＡＢＦ≡△ＣＤＧ。
（２） 34.8％
ポイントは（１）の△ＡＢＦ≡△ＣＤＧを用いること。
平行四辺形ＡＢＣＤ＝△ＡＢＦ＋四角形ＡＦＣＤ＝△ＣＤＧ＋四角形ＡＦＣＤ＝五角形ＡＦＣＧＤ
△ＣＥＧ＝四角形ＡＦＥＤ－五角形ＡＦＣＧＤ＝ｂ－ａｃｍ2
（３）① 77.7％
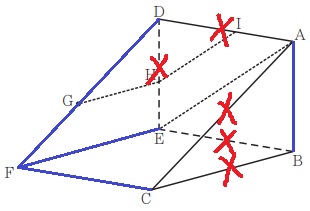
ネジレではないものを省く。
辺ＡＤは交わる。辺ＤＥは平行。
イ・エ・オ
② 39.8％
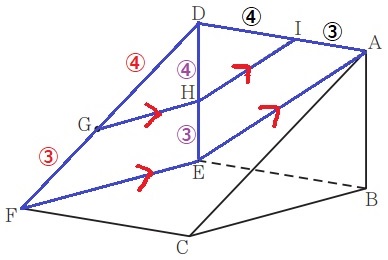
ＧＨ//ＦＥ、ＨＩ//ＥＡから４：３を移す。
ＤＧ：ＧＦ＝ＤＨ：ＨＥ＝ＤＩ：ＩＡ＝４：３
ＤＡ＝６ｃｍだから、ＤＩ＝６×④/⑦＝24/７ｃｍ
（４） 5.9％!!
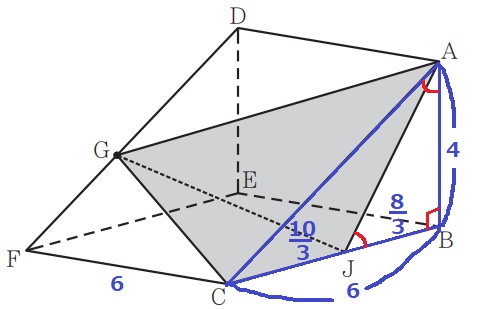
三角柱なので、面ＡＢＣ⊥面ＦＣＡＤ。
三角錐Ｇ－ＡＣＧの底面を△ＡＣＪとすると、高さはＦＣ＝６ｃｍにあたる。
△ＡＣＪの面積が知りたい。
与えられた等角から２角が等しく、△ＡＢＣ∽△ＪＢＡ。
ＡＢ：ＢＣ＝ＪＢ：ＢＡ＝４：６＝２：３
ＪＢ＝４×２/３＝８/３ｃｍ
ＣＪ＝６－８/３＝10/３ｃｍ
したがって、三角錐Ｇ－ＡＣＧの体積は、10/３×４÷２×６÷３＝40/３ｃｍ3
大問１
失点注意！
（８）小数の計算です。
（９）４の倍数でない偶数。
４を弾き、６と奇数の組み合わせが答えとなる。
（10）体積比の処理に慣れておこう。
大問２
（１）高い正答率◎
（２）条件把握。問題文が変にややこしく書かれてある。
間の数は花の本数－１である。
大問３
（２）ＦＤの長さをｔで表し、これがＤとＥのｙ座標の差であることから立式。
大問４
（１）直角三角形の合同条件を疑う。
（２）前問の合同を用いて平行四辺形ＡＢＣＤを変形させる。
（３）②４：３が維持される。
（４）△ＡＣＪが△ＡＢＣにベッタリくっついているので、これが底辺となる。
あとはどうやってＣＪを求めるか。ＢＣが６だからＪＢがわかればいい。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント