平均61.4点（前年比；－2.8点）
問題はコチラ→ＰＤＦファイル
Ｂ問題、Ｃ問題の解説はコチラ。
大問１（計算）
（１） 84.0％
－７－10
＝－17
（２） 76.7％
８/７÷（－４）
＝－２/７
（３） 90.7％
３×（－２）2
＝３×４＝12
（４） 69.3％
ｘ＋４＋５（ｘ－３）
＝ｘ＋４＋５ｘ－15
＝６ｘ－11
（５） 91.8％
ｘｙ×２ｙ
＝２ｘｙ2
（６） 79.3％
√45＋５√５
＝３√５＋５√５
＝８√５
大問２（小問集合）
（１） 71.3％
２ａ＋７
＝２×（－８）＋７
＝－16＋７＝－９
（２） 69.3％
4.6－（－1.3）
＝4.6＋1.3＝5.9℃
（３） 39.3％
ア：ｙ＝６ｘ＋30…一次関数×
イ：ｙ＝500/ｘ…反比例×
ウ：ｙ＝－ｘ＋140…一次関数×
エ：ｙ＝25ｘ…比例〇
（４） 65.8％
５ｘ＋ｙ＝22…①
＋)ｘ－ｙ＝－４…②
６ｘ ＝18
ｘ＝３
②に代入。ｙ＝３＋４＝７
ｘ＝３、ｙ＝７
（５） 47.6％
ｘ2＋３ｘ－10
＝（ｘ＋５）（ｘ－２）＝０
ｘ＝－５、２
（６） 50.0％
和が８となる場合は、
（２、６）（３、５）（４、４）（５、３）（６、２）の５通り。
５/36
（７） 42.0％
ア：シュート９本は１年生で１人、２年生で０人×
イ：範囲（レンジ）＝最大値－最小値
１年生は９－６＝３本、２年生は10－５＝５本で異なる×
ウ：１年生９人の中央値（メジアン）は５番目→７本
２年生11人の中央値は６番目→７本〇
エ：１年生の最頻値（モード）は７本、２年生は８本×
ウ
（８）① 54.9％
ｙ＝１/２ｘ2にｘ＝－４を代入。
ｙ＝１/２×（－４）2＝８
② 18.9％！
ａ＞０なので、下に凸のグラフとなる。
ｘ＝０のとき、最小値ｙ＝０
ｘ＝３のとき、最大値ｙ＝９/２
０≦ｙ≦９/２
ア…０、イ…９/２
（９）① 96.7％
（え）を床にすると、（い）と（か）が左右の壁になる。
イ
② 45.8％
（か）を底辺とすると、１辺ａｃｍの正方形で高さが５ｃｍの直方体。
ａ×ａ×５＝５ａ2ｃｍ3
大問３（数量変化）
（１）ア…90.7％、イ…86.0％
はじめに４秒。写真の枚数×５秒が加算される。
（ア）＝４＋５×４＝24
（イ）＝４＋５×７＝39
（２） 46.7％
ｙ＝５秒×写真ｘ枚＋タイトル４秒
ｙ＝５ｘ＋４
（３） 74.0％
上の式にｙ＝84を代入。
５ｘ＋４＝84
５ｘ＝80
ｘ＝16
大問４（平面図形）
（１） 41.6％
ＡＣは１辺９ｃｍの正方形の対角線。
１：１：√２より、ＡＣ＝９√２ｃｍ
（２） 17.3％！
半径９ｃｍ、中心角90°の扇形の面積。
９×９×π×１/４＝81π/４ｃｍ2
（３）ａ…44.7％、ｂ…71.3％、ｃ…38.0％
△ＣＨＢ≡△ＥＦＣの証明。
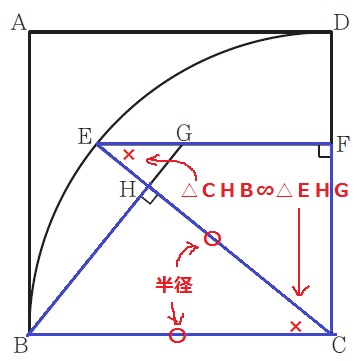
半径より、ＢＣ＝ＣＥ
∠ＣＨＢ＝∠ＥＦＣ＝90°
△ＣＨＢ∽△ＥＨＧより、∠ＢＣＨ＝∠ＣＥＦ
以上より、直角三角形の斜辺と１鋭角が等しいので合同。
ａ…ＣＥ、ｂ…ＣＥＦ、ｃ…イ
*別の表現でも辺や角が特定できれば〇がもらえるが、
なるべく対応する順に記号を書いた方がいいかもしれない。
問題文では△ＣＨＢ∽△ＥＨＧが与えられていたが、
これは∠ＤＦＥ＝∠ＦＣＢ＝90°で同位角が等しく、
ＥＦ//ＢＣ→錯角が等しいことから２角相等より導ける。
（４） 4.3％!!
答案では過程も記述する。
△ＣＨＢ≡△ＥＦＣより、ＣＨ＝７ｃｍ
ＥＨ＝９－７＝２ｃｍ
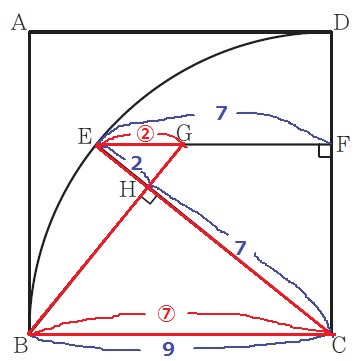
ここで△ＣＨＢ∽△ＥＨＧを使う。
ＥＧ：ＣＢ＝ＥＨ：ＣＨ＝２：７
ＥＧ＝９×２/７＝18/７ｃｍ
ＧＦ＝７－18/７＝31/７ｃｍ
＠別解＠
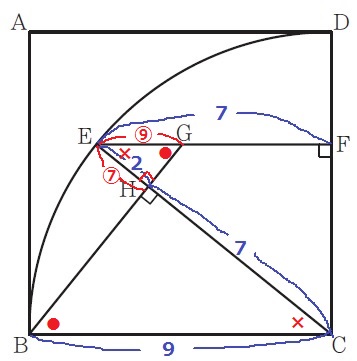
△ＣＨＢ∽△ＥＨＧで、ＥＨ：ＥＧ＝ＣＨ：ＣＢ＝７：９でもＯＫ。
ＥＧ＝２×９/７＝18/７ｃｍ
ＧＦ＝７－18/７＝31/７ｃｍ
大問１
数学が苦手な人も計算だけはしっかりやっておきたい。
大問２
（３）式で表す。比例に切片ｂがついたら一次関数。
（８）②変域問題はどこの都道府県でも出してくる。
迷ったらグラフを描いてみよう。
大問３
一応（２）が前提なのだが、（３）の方が正答率がいい･･。
大問４
（３）まで粘りたい。
（２）の正答率が２割を切っていたが、単純に扇形の面積を求めるだけ。
扇形のなかにある線分は関係無い。見た目に騙されてはいけない。
公立高校入試解説ページに戻る
コメント