平均57.0点(前年比;+19.9点)
問題はこちら→東進ハイスクールさん(解答)
出題範囲の除外は円周角と中心角、三平方の定理、資料の活用。
2021年大阪A問題、2021年大阪B問題の解説は別ページ。
大問1(小問集合)
(1) 96.2%
(7a+b)/3-(3a-5b)/2
={2(7a+b)-3(3a-5b)}/6
=(14a+2b-9a+15b)/6
=(5a+17b)/6
(2) 96.2%
(3/4ab)2÷9/8a2b×(-2b)

=-b2
(3) 98.1%
√3(√15+√3)-10/√5
=3√5+3-2√5
=3+√5
(4) 73.8%
2(a+b)2-8
=2{(a+b)2-22}
=2(a+b+2)(a+b-2)
(5) 69.8%
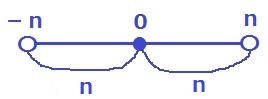
両端は含まないので-1する!
n-(-n)-1=2n-1個
*n=3で検算。-2~2の5個。2×3-1=5個
(6) 96.2%
1つの外角は、180-140=40°
n角形の外角の和は360°だから、360÷40=9
九角形の内角の和を求めればいい。
n角形の内角の和は180(n-2)°なので、
180×(9-2)=1260°
(7) 26.7%!
a=-1で試してみる。
ア:-1+2=1×
イ:-1-2=-3〇
ウ:-1×2=-2〇
エ:-1<-1/2×
オ:-1=-1であってそう。。
しかし、a=-0.1のとき-a2=-0.01となり、-0.1<-0.01×
イ・ウ
(8) 94.3%
Bを仮の平均とする。
(+5+0-3-6+2)÷5人=-0.4回
(仮の平均B)-0.4=47.6回なので、
Bの回数は、47.6+0.4=48回
(9) 48.6%
6枚から2枚を取り出す→6C2=15通り
◆黒が3枚連続
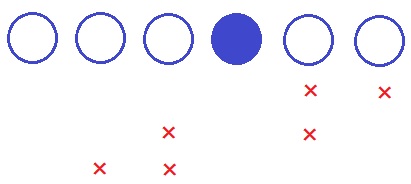
3通り
◆白が3枚以上
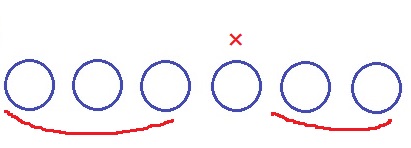
最初に左から4番目を裏返して白にする。
残りの1枚は何でもいい→5通り
計8通り、確率は8/15
(10) 62.4%

ルートを外すには、100-nは3の倍数でなくてはならない。
また、偶数にするので偶数の平方数でもある(平方数でないとルートが外れない)
◆100-n=3×2×2
n=88
◆100-n=3×4×4
n=52
◆100-n=3×6×6
nは2桁の自然数なので、これ以上はない。
n=52、88
(11) 54.3%
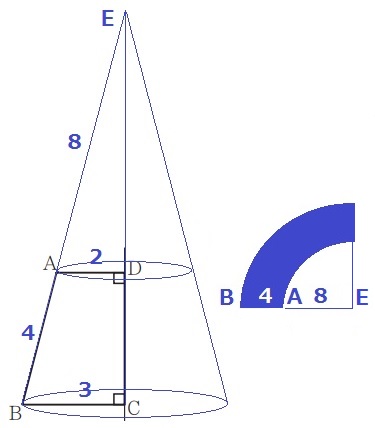
回転体は円錐台(プリン型)
円錐の頂点をEとする。
△EAD∽△EBCの相似比は2:3→EA=8cm
回転体の上は半径2cmの円、下は半径3cmの円。
側面は半径12cmの扇形から半径8cmの扇形を引く。
扇形の側面積→母線×半径×π
2×2×π+3×3×π+(12×3×π-8×2×π)
=33πcm2
大問2(関数)
(1)① 89.5%
y=3/8x2において、
x=0のとき、最小値y=0
x=-3のとき、最大値y=27/8
ア…0、イ…27/8
② 92.4%
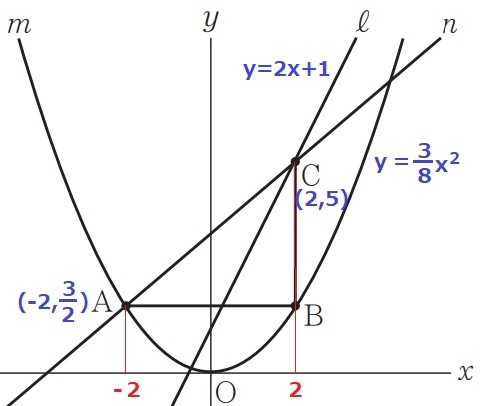
y=3/8x2にx=-2を代入→A(-2、3/2)
ABはx軸に平行で、AとBはy軸について対称な点→Bのx座標は2
y=2x+1にx=2を代入→C(2、5)
ACの傾きは、(5-3/2)÷{2-(-2)}=7/8
y=7/8x+bにCの座標(2、5)を代入。
5=7/8×2+b
b=13/4
y=7/8x+13/4
(2) 36.3%
答案では求め方も記述する。
方針はD→F→Gの順で座標を確定する。
FはP上の点。GとFはy座標を共通とする。
G座標をaで表せば、直線ℓの式からaの値が判明する。

y=3/8x2にy=6を代入→D(4、6)
Fのx座標は4。y=ax2に代入して、F(4、16a)
a<0よりEF=-16a、GF=-16a+2
Gのx座標は、4-(-16a+2)=16a+2
G(16a+2、16a)
これを直線ℓに代入。
16a=2(16a+2)+1
a=-5/16
大問3(図形)
(1) 61.9%
△AEG∽△FCGの証明。

対頂角より、∠AGE=∠FGC
二等辺三角形ABCの底角と三角形の合同から、∠ACB=∠CAE
錯角が等しいので、AE//BF
錯角で∠GEA=∠GCF
2角が等しく∽
(2) 17.1%!
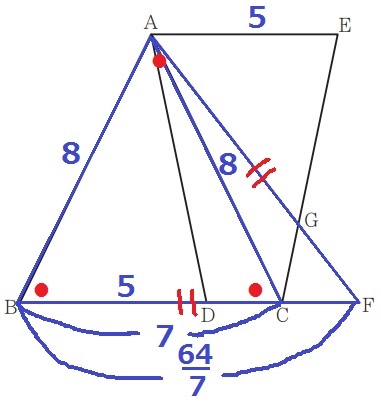
ポイントは二等辺ABCと二等辺FBAの底角である∠ABC=∠FBA
ここから△ABC∽△FBAが導ける。相似比はBC:BA=7:8
FB=FA=8×8/7=64/7cm
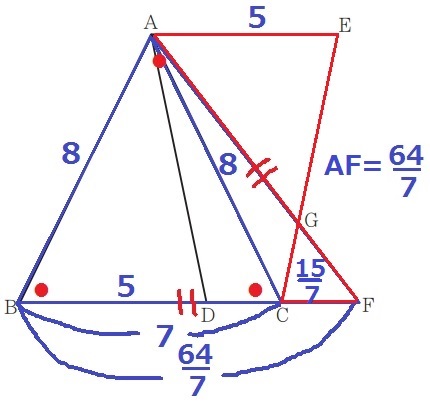
FC=64/7-7=15/7cm
△AGE∽△FGCより、AG:GF=AE:FC=5:15/7=7:3
GF=64/7×3/10=96/35cm
(3) 45.7%

↑展開するとこうなる。
面積比は相似比の2乗。
△AEF:△ABC=1:4なので、
△AEFの面積をSとすると、四角形EBCFの面積は3S
△ABDと△ABCは高さが同じで、面積比は底辺の6:8=3:4である。
△ABD:△ABC=△AEG:△AEF=四角形EBDG:四角形EBCF=3:4
四角形EBDGの面積は、3S×3/4=9/4Scm2
(4) 20.5%!
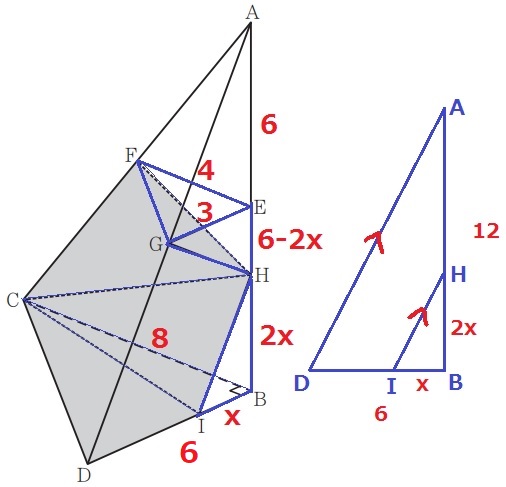
E・F・Gは中点だから、中点連結定理よりEF=4cm、EG=3cm
三角錐A-EFG:三角錐A-BCDの体積比は1:8
角錐台EFG-BCDの体積は、6×8÷2×12÷3×7/8=84cm3
三角錐H-EFGと三角錐H-BCIの体積の合計は、84-70=14cm3
また、AD//HIから△ABD∽△HBI
AB:BD=HB:BI=12:6=2:1
求める長さはHBだが、長さの短いIB=xcmとする。
HB=2xcm、EH=6-2xcm
2つの三角錐の体積の和で等式を立てる。
{2x×x÷2×8+3×(6-2x)÷2×4}÷3=14
8x2+36-12x=42
8x2-12x-6=0
4x2-6x-3=0
解の公式を適用。b=2b’が使える。
x=(3±√21)/4
IB>0より、x=(3+√21)/4
HB=(3+√21)/4×2=(3+√21)/2cm
●講評●
大問1
大阪Cは激戦ゆえ、計算問題でミスができない。
(7)数直線で考えると良いかも。オはaが1未満だと0に近づく。
(9)黒3枚か白3枚以上で場合分け。短時間で調べられる。
(11)B問題では体積であった。
大問2
(2)座標と距離の関係に注意。
大問3
(2)本問が最も正答率が低かった。
二等辺の∽が見えづらかったか。
(4)角錐台から2つの三角錐をひいて70cm3
あとは頑張って等式を立てる。



コメント