合格者平均；53.0点
問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）① 91.4％
６－９－（－２）
＝－３＋２＝－１
② 77.3％
（－２/５＋４/３）÷４/５
＝－２/５÷４/５＋４/３÷４/５ ←分配法則
＝－１/２＋５/３
＝７/６
③ 64.7％
（－３ａ）2÷６ａｂ×（－16ａｂ2）
＝－24ａ2ｂ
④ 76.6％
（√３＋１）（√３＋５）－√48
＝８＋６√３－４√３
＝８＋２√３
（２） 79.5％
答案では解き方も記述する。
（２ｘ－１）（ｘ－４）＝－４ｘ＋２
２ｘ2－９ｘ＋４＝－４ｘ＋２
２ｘ2－５ｘ＋２
＝（２ｘ－１）（ｘ－２）＝０
ｘ＝１/２、２
（３） 51.4％
すべての場合は、２×３×３＝18通り
『少なくとも１個は白』＝すべて－全部白
全部白の場合は、１×１×２＝２通り
『少なくとも１個は白』…18－２＝16通り
確率は、16/18＝８/９
（４） 46.8％
円錐の側面積となる扇形の中心角は【×半径/母線】で処理。
360×５/10＝180°
半円であるウ。
（５） 48.2％
ア：最頻値は１組…7.75時間、２組…7.75時間で同じ。×
イ：１組…32人の中央値は16番目と17番目の平均で7.25時間。
２組…33人の中央値は17番目で7.75時間。２組の方が大きい。×
ウ：１組…７人、２組…11人で２組のほうが多い。×
エ：１組…21/32、２組…21/33
分子が同じ。分母が小さい１組の方が値が大きい。〇
エ
大問２（小問集合２）
（１）① 52.9％
反比例の変化の割合。
ｘ＝１のとき、ｙ＝12
ｘ＝４のとき、ｙ＝３
変化の割合＝（ｙの増加量）/（ｘの増加量）
＝（３－12）/（４－１）＝－３
② 46.8％
ｙ＝12/ｘにｘ＝３を代入して、Ａ（３、４）。
これをｙ＝ａｘ2に代入してａを求める。
４＝９ａ
ａ＝４/９
ｙ＝４/９ｘ2にｘ＝－６を代入して、Ｂ（－６、16）。
直角三角形をつくると、辺の比が３：４：５。
ＡＢ＝15
（２）得点率100％－19.8％！、50～99％－14.7％、１～49％－14.4％
整数の証明問題。
４けたの自然数は、1000ａ＋100ｂ＋10ａ＋ｂと表すことができる。
1000ａ＋100ｂ＋10ａ＋ｂ
＝1010ａ＋101ｂ＝101（10ａ＋ｂ）
10ａ＋ｂが整数だから、101（10ａ＋ｂ）は101の倍数である。
（３）① 64.0％
観戦者の人数をｘとおく。最初に持っていた金額で等式を立てる。
3300ｘ－4400＝2700ｘ＋400
*過不足の扱いに注意しよう！
連立の場合は、最初に持っていた金額をｙ円とし、
ｙ＝3300ｘ－4400
ｙ＝2700ｘ＋400
② 55.4％
うえの一次方程式を解く。
600ｘ＝4800
ｘ＝８
最初に持っていた金額は、2700×８＋400＝22000円
（４） 57.9％
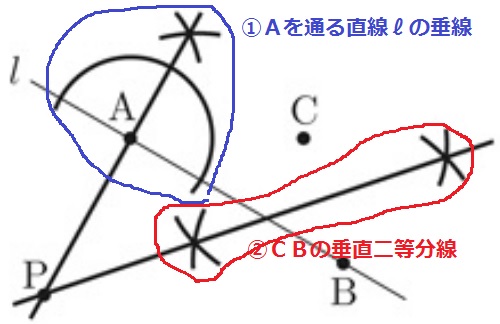
①『点Ａで直線ℓと接する円』→中心から伸びる半径と接線は直交する→Ａを通る直線ℓの垂線
②『２点Ｂ、Ｃを通る円』→ＢＣの垂直二等分線
これらの交点が２つの円の中心Ｐ。
大問３（数量変化）
（１）① 76.3％
動く距離が４ｃｍになるまで、重なる部分は正方形。
ｙ＝３×３＝９
②ア；74.8％、イ；57.9％、ウ；45.3％、グラフ；76.6％
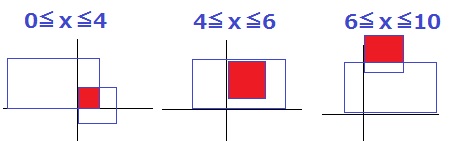
０≦ｘ≦４のとき、１辺がｘの正方形。ｙ＝ｘ2
ｘ＝４のとき、１辺４ｃｍの正方形（ｙ＝16）がスポっと入る。
正方形が長方形ＰＱＲＳから出る直前は辺ＡＤが辺ＰＳに接したとき。
それまで重なる部分は16で一定。
４≦ｘ≦６のとき、ｙ＝16
６≦ｘ≦10のときの式を求める。
ｘ＝６のとき、ｙ＝16
ｘ＝10のとき、ｙ＝０
（６、16）（10、０）の２点を通る式。
傾きは、（０－16）÷（10－６）＝－４
０＝－４×10＝ｂ
ｂ＝40
ｙ＝－４ｘ＋40
ア…６、イ…ｘ2、ウ…４ｘ＋40
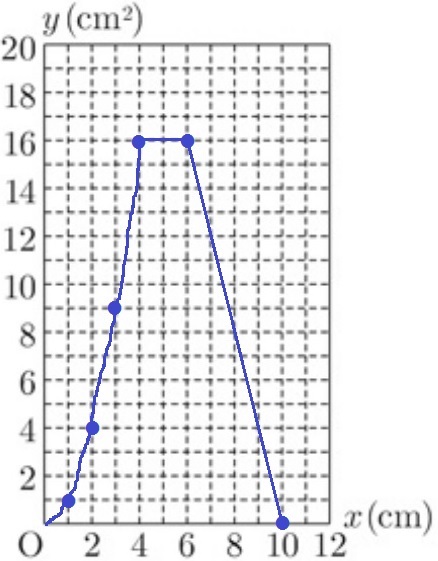
最初はｙ＝ｘ2なので、（１、１）（２、４）（３、９）の格子点を通過するように描く。
（２） 9.4％!!
重なっている部分ｙと△ＡＰＱの面積が等しくなる瞬間はどこか？
ｘ＝４のとき、ｙ＝16
試しに、このときの△ＡＰＱの面積を求めると、
ＰＱ×ＱＯ÷２＝６×（10－４）÷２＝18
ということは、０≦ｘ≦４では等しくならない。
今度は次の転換点であるｘ＝６のときを計算すると、
△ＡＰＱの面積は、４×（10－６）÷２＝８
４≦ｘ≦６のとき、重なっている部分ｙは16で一定なので、この変域のどこか。
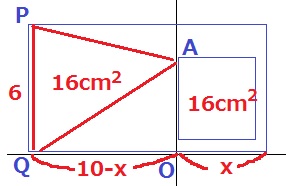
６×（10－ｘ）÷２＝16
30－３ｘ＝16
ｘ＝14/３
大問４（平面図形）
（１）100％—14.4％！、50～99％—13.7％，１～49％—50.0％
△ＡＣＧ≡△ＡＤＥの証明。
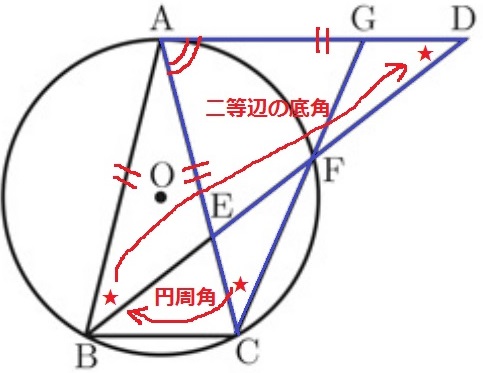
仮定から、ＡＣ＝ＡＤ。この両端角に狙いを定める。
共通角で∠ＣＡＧ＝∠ＤＡＥ
弧ＡＦの円周角→ＡＢ＝ＡＤより△ＡＢＤは二等辺三角形→∠ＡＣＧ＝∠ＡＤＥ
１辺と両端角相等で合同。
*平行線は使わなかった。
（２）① 49.6％
△ＡＤＥ∽△ＣＢＥ。
ＡＥ：ＣＥ＝ＡＤ：ＣＢ＝６：３＝２：１
ＡＣ＝６ｃｍなので、ＡＥ＝６×２/３＝４ｃｍ
＠別解＠
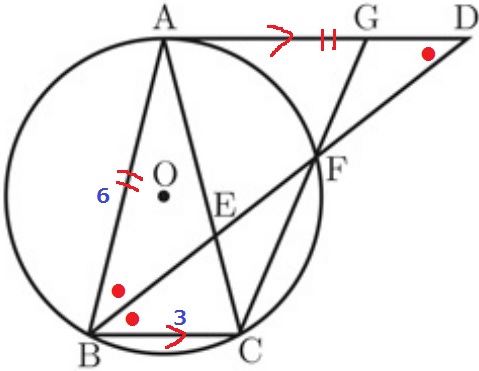
二等辺三角形ＡＢＤの底角と、平行線→錯角で∠ＡＢＥ＝∠ＥＢＣ
角の二等分線の定理より、ＢＡ：ＢＣ＝ＡＥ：ＥＣ＝６：３＝２：１
ＡＥ＝６×２/３＝４ｃｍ
② 2.2％!!
△ＡＢＥと△ＣＥＦは対頂角と円周角で２角が等しく相似。
辺の比さえわかれば、隣辺比の積から面積比が出せる。
ＦＣ：ＦＥ＝ＡＢ：ＡＥ＝６：４＝③：②
ＢＥの値を出せないものか？
等角の●に注目して共通角と合わせると、△ＢＣＦ∽△ＣＥＦ
ＢＣ：ＢＦ＝ＣＥ：ＣＦ
３：ＢＦ＝２：③
ＢＦ＝③×３/２＝〇4.5
ＢＥ＝〇4.5－②＝〇2.5
隣辺比から面積比。
△ＡＢＥ：△ＣＥＦ
＝ＡＥ×ＢＥ：ＦＥ×ＣＥ
＝４×〇2.5：②×２
＝10：４
＝５：２
＠別解＠
（１）の△ＡＣＧ≡△ＡＤＥから、ＡＧ＝ＡＥ＝４ｃｍ、ＧＤ＝６－４＝２ｃｍ
２つの合同図形から斜線部分を除くと、余りの△ＣＥＦと△ＤＧＦも合同。
ＤＦ＝③
△ＢＣＦ∽△ＤＧＦより、ＢＦ＝③×３/２＝〇4.5
ＢＥ＝〇4.5－②＝〇2.5
あとは先ほどと同様に隣辺比で５：２。
大問１
（３）『少なくとも』ときたら余事象の確率。
（４）×半径/母線は他でもでるよ！取れないのはもったいない。
（５）機械的に調べるだけ。もう少し正答率を上げたい。
大問２
（１）①大阪Ｃでも反比例の変化の割合が出た。
（２）数を文字式で表す→101でまとめる→お決まりの常套句を披露。
大問３
（１）②グラフの方が正答率高いのは何故？
混乱したら絵を描いて整理する。
（２）まず、どのｘの変域に答えが含まれるか。
転換点ごとに△ＡＰＱの面積を算出して絞る。
大問４
似たような図形を他でも見かけた気がする。
（２）②隣辺比の処理に慣れておきたい。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント
こんにちは。先生の解法で、隣辺比の積は、面積比を使って解ける解法は、とても素晴らしいと思います。中学入試では、図形問題の面積比を求める問題では、この「隣辺比の積は面積比」にんじん慣れると、難しい面積比の問題も素早く解けるので、とても良いと思います。先生の解法を参考にする受験生が増える事を願っています。ただ、この「隣辺比の積は面積比」は、現在の小学校・中学校の学習指導要領にないため、「隣辺比の積は面積比」を知らない生徒は、どのように解くのだろうか。その一例としてサボ先生の解法を使わせてもらえますと、次のような解法が考えられるかと思います。
[隣辺比の積は面積比を知らない場合の解法例]山形県公立高校数学入試大問4の最後の問題で、示してみたいと思います。
AE:EC=２:1より、△BCE=Sとすると、△ABEは=２Sである。また、△BCE:△CEF=
S:△CEF=◯2.5:◯2=◯5:◯4より、
△CEF=4S/5である。△ABE:△CEF=２S:4S/5=10:4=5:２よって、答え 5:２
以上ですが、やはり、サボ先生の解法の「隣辺比の積は面積比」に慣れる方が、入試対策としては、とても良い解き方と思います。これからも、受験生のために、尽力をいただけますと、嬉しく存じます。これからも宜しくお願いします。お助けマンより。