2021年度　聖光学院中学過去問【算数】大問３解説

問題ＰＤＦ
Ａ地点とＢ地点の間を聖たかしさん、光さん、学さんの３人が移動します。聖さんはＡ地点を午前８時３分に出発し、Ｂ地点へ向かいました。また、学さんと光さんは、この順にそれぞれ別の時刻にＢ地点を出発し、Ａ地点へ向かいました。すると、聖さんが出発してから７分30秒後に、聖さん、光さん、学さんの３人は、Ａ地点とＢ地点の間のＣ地点を同時に通過しました。
光さんは午前８時15分30秒にＡ地点に着いて、しばらく休憩したあとにＢ地点に向かって出発しました。また、聖さんはＢ地点に着いてしばらく休憩したあと、午前８時20分にＡ地点に向かって出発しました。２人が休憩した時間は、光さんより聖さんのほうが２分30秒だけ長かったことが分かっています。
光さんはＡ地点を出発してしばらくすると学さんとすれ違い、さらにその３分36秒後に聖さんとすれ違い、午前８時26分にＢ地点に着きました。３人の速さはそれぞれ一定であるものとして、次の問いに答えなさい。

（１）
聖さんと光さんの速さの比を最も簡単な整数比で答えなさい。

（２）
聖さんがＢ地点に着いたのは、午前何時何分ですか。

（３）
光さんがＢ地点を出発したのは、午前何時何分何秒ですか。

（４）
学さんがＢ地点を出発したのは、午前何時何分ですか。

＠解説＠

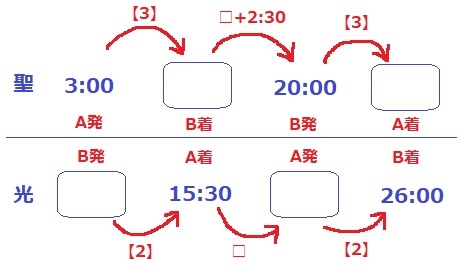
↑聖と光のダイヤグラムを示すとこうなる。
時間はすべて午前８時なので分と秒のみ記載している。
この問題のイヤのところは光の出発時刻が不明なこと。。
（最初は適当に描くしかない）
光の休憩時間を□とすると、聖の休憩時間は□＋２分30秒。

（１）

ＡＣ間を聖は７分30秒間、光は15：30－３：00－７分30秒＝５分間で移動する。
時間の比は、聖：光＝7.5分：５分＝３：２
速さの比は逆比で２：３。

（２）
ここで差がつく。

休憩時間をうまく使うしかない。
片道にかかる時間の比は、聖が【３】、光が【２】
聖のＡ発～Ｂ発は、20：00－３：00＝17分間
【３】＋□＋２分30秒＝17分
【３】＋□＝14分30秒　…①

光のＡ着～Ｂ着は、26：00－15：30＝10分30秒間
【２】＋□＝10分30秒　…②

①－②
【３】＋□＝14分30秒
－)【２】＋□＝10分30秒
【１】　　＝４分

聖は【３】＝12分かかるので、
聖がＢに着いたのは、８時３分の12分後→午前８時15分

（３）
光は【２】＝８分
光がＢを出発したのは、８時15分30秒の８分前→午前８時７分30秒

（４）
（２）②の【２】＋□＝10分30秒に、【２】＝８分を代入すると、
□＝10分30秒－８分＝２分30秒
光の休憩時間は２分30秒、聖の休憩時間は５分となる。

使っていない情報は『光がＡ地点を出発して学とすれ違った３分36秒後に聖とすれ違う』

時間の比は聖：光＝〔３〕：〔２〕
８時20分～26分の６分間を３：２に案文する。
光と聖がすれ違った時刻は、20：00＋６分×３/５＝23：36
その３分36秒前は、ちょうど聖がＢ地点を出発した８時20分にあたる。

光と学がすれ違った場所をＤとする。
ＣＤ間の時間を計算する。
光はＢＣ間を３分、ＡＤ間を２分で移動するので、ＣＤ間は８－（３＋２）＝３分
学は20：00－10：30＝９分30秒

【光が３分で進む距離を学は９分30秒かかる】

ここで、ＢＣ間に注目する。
光は７：30にＢを出発し、ＢＣ間をちょうど３分で移動している。
ということは、学はＢＣ間を９分30秒で移動した。
学がＢを出発したのは、８時10分30秒の９分30秒前→午前８時１分
難関中（算数科）解説ページに戻る