2023年度　大阪府公立高校入試Ａ問題過去問【数学】解説

平均48.9点（前年比；－9.3点）
問題はコチラ→ＰＤＦファイル
2023年度・大阪（数学）Ｂ問題、Ｃ問題の解説はコチラ。

大問１（計算）

（１）　77.4％
５×（－４）＋７
＝－20＋７
＝－13

（２）　72.9％
3.4－（－2.5）
＝3.4＋2.5
＝5.9

（３）　90.3％
２×４²
＝２×16
＝32

（４）　58.1％
８ｘ－３＋２（ｘ＋１）
＝８ｘ－３＋２ｘ＋２
＝10ｘ－１

（５）　75.5％
－18ｘｙ÷３ｘ
＝－６ｙ

（６）　48.4％
√５＋√45
＝√５＋３√５
＝４√５

大問２（小問集合）

（１）　32.3％！
－７/４＝－１・３/４
－２と－１のあいだ。
ウ

（２）　58.1％
４ａ＋21
＝４×（ー３）＋21
＝－12＋21
＝９

（３）　54.2％
３の倍数になる⇒３でくくれる。
３ｎ＋６＝３（ｎ＋２）
ｎは整数だから、ｎ＋２は整数。
３（ｎ＋２）は整数ｎ＋２を３倍した数＝３の倍数
エ

（４）　44.3％
文字式の基本。
２ａ＋７ｂｇ

（５）　38.7％
ｎ角形の内角の和は180（ｎ－２）°
180×（５－２）＝540°

（６）　3.9％!!
四分位範囲＝第３四分位数－第１四分位数＝55－50＝５回

＠四分位範囲＠
データ全体のうち、真ん中に集まる約50％の散らばり具合を示す。
真ん中から離れた極端な値を排除する点が強み。

（７）　45.8％
ｘ－３ｙ＝10　…①
５ｘ＋３ｙ＝14　…②
①＋②で、６ｘ＝24
ｘ＝４
①に代入、４－３ｙ＝10
ｙ＝－２
ｘ＝４、ｙ＝－２

（８）　38.7％
ｘ²－２ｘ－35
＝（ｘ＋５）（ｘ－７）＝０
ｘ＝－５、７

（９）　11.6％！
全体は、６×６＝36通り
出目の和が10より大きい→和が11か12
和が11は（５、６）（６、５）、和が12は（６、６）の３通り。
確率は、３/36＝１/12

（10）　2.6％!!
　
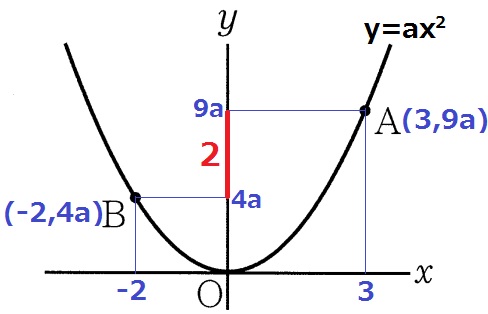
ｙ＝ａｘ²にｘ座標を代入。
各々のｙ座標はＡが９ａ、Ｂが４ａ。
９ａ－４ａ＝５ａ＝２
ａ＝２/５

（11）　14.8％！

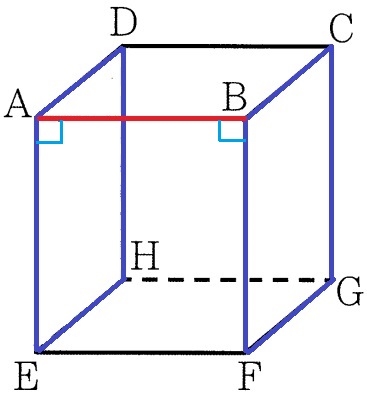
辺ＡＢと垂直な面は面ＡＥＨＤと面ＢＦＧＣ。
イ

大問３（数量変化）

（１）①ア…71.6％、イ…53.5％

ｘが１が増えるとｙは６減る。
ｘ＝３のとき、ｙ＝840－６×３＝822
ｘ＝９のとき、ｙ＝840－６×９＝786
ア…822、イ…786

②　29.7％！
ｘが１増えるとｙは６減る⇒傾きは－６
切片はｘ＝０のときのｙ＝840
ｙ＝－６ｘ＋840

（２）　38.5％
ｙ＝－６ｘ＋840にｘ＝ｔ、ｙ＝450を代入。
450＝－６ｔ＋840
６ｔ＝390
ｔ＝65

大問４（平面図形）

（１）　9.7％!!

回転体は円錐。
エ

（２）　6.5％!!
平行四辺形ＡＢＣＤの対辺は等しい。
ＢＣ＝ＡＤ＝８ｃｍ
平行四辺形ＡＢＣＤの底辺ＢＣは８ｃｍ、高さＤＧはｘｃｍなので、
面積は８ｘｃｍ²

（３）ａ…64.5％、ｂ…27.1％！、ｃ…46.5％
△ＥＡＤ∽△ＧＣＤの証明。

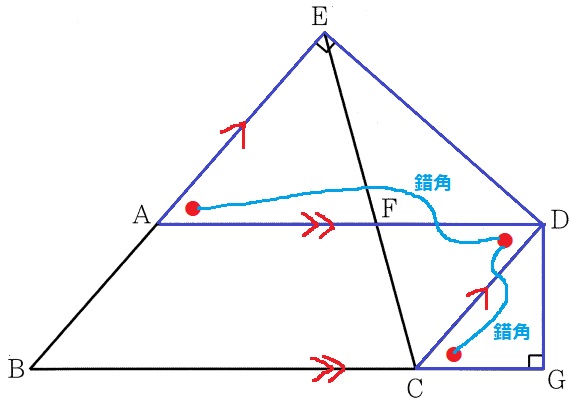
∠ＤＥＡ＝∠ＤＧＣ＝90°　…①
ＥＢ//ＤＣの錯角で、∠ＥＡＤ＝∠ＡＤＣ　…②
ＡＤ//ＢＧの錯角で、∠ＧＣＤ＝∠ＡＤＣ　…③
②、③より、∠ＥＡＤ＝∠ＧＣＤ　…④
①、④より、２角が等しいから相似。
ａ…ＤＧＣ、ｂ…ＧＣＤ、ｃ…ウ

（４）　1.8％!!
答案では求める過程も記述する。

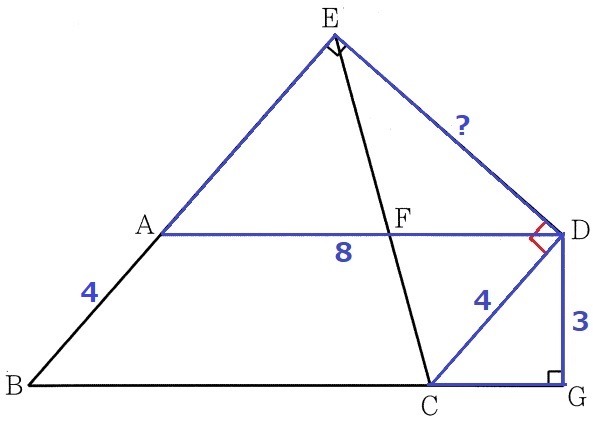
問題文にあるようにＥＤ⊥ＤＣ（∠ＤＥＡ＝90°とＥＢ//ＤＣから導ける）。
ＥＤがわかれば、△ＣＤＥで三平方の定理を使ってＥＣが求まる。

ＥＤは△ＥＡＤの辺だから、前問の△ＥＡＤ∽△ＧＣＤを使う。
平行四辺形の対辺は等しいので、ＤＣ＝ＡＢ＝４ｃｍ
△ＥＡＤ∽△ＧＣＤより、ＤＥ：ＤＧ＝ＤＡ：ＤＣ＝２：１
ＤＥ＝３×２＝６ｃｍ
△ＣＤＥで三平方→ＥＣ＝２√13ｃｍ

2023年度・大阪（数学）Ｂ問題、Ｃ問題の解説はコチラ。
公立高校入試解説ページに戻る