問題ＰＤＦ
４桁の整数Ｍと４桁の整数Ｎがあります。
この２つの整数について次の性質の一部、もしくは全部が成り立っています。
性質① Ｍを４倍するとＮになる。
性質② Ｍの千の位とＮの百の位は等しく、また、Ｍの百の位とＮの千の位は等しい。
性質③ Ｍの十の位とＮの一の位は等しく、また、Ｍの一の位とＮの十の位は等しい。
このとき、次の各問いに答えなさい。
（１）
性質①が成り立つとき、Ｍとして考えられる整数は何個ですか。
（２）
性質①と性質②が成り立つとき、
Ｍの十の位以下を切り捨てた値として考えられる整数をすべて答えなさい。
（３）
性質①と性質②と性質③が成り立つとき、
Ｍとして考えられる整数をすべて答えなさい。
＠解説＠
（１）
2500×４＝10000だから、４倍して４桁となる最大数は2499。
1000～2499の1500個。
（２）
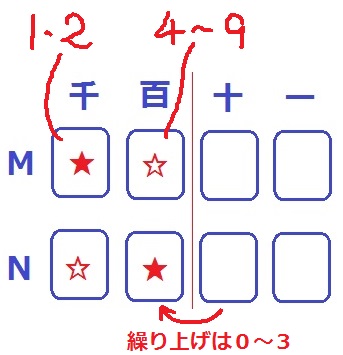
十の位以下は切り捨てるので、百の位と千の位の数字だけを考える。
★と☆には同じ数字がはいる。
先ほど、Ｍは1000～2499の1500個しかないとわかったので、
Ｍの千の位から★には１か２しか入らない！
Ｎの最小値は1000×４＝4000
最大値は2499×４＝（2500－１）×４＝9996
Ｎの千の位から☆には４～９しか入らない！
また、４×９＝36ゆえ、十の位からの繰り上げは０～３の範囲に絞られる。
…パターンが少ないので、Ｍの千の位★と百の位☆に４をかけて試す。
14×４＝54
→54〇〇だから、Ｎは41〇〇にならない×
15×４＝60
→百の位が４未満×。Ｎは06〇〇になってしまう。
16×４＝64
→64〇〇だから、Ｎは61〇〇にならない×
17×４＝68
→68に繰り上がり３を足すと71で、Ｎは71〇〇になりうる〇
18×４＝72
→Ｎは81〇〇にならない×
19×４＝76
→Ｎは91〇〇にならない×
24×４＝96
→Ｎは42〇〇にならない×
すべて答えなさいだが、Ｍは17〇〇しかない。
十の位は切り捨てなので、答えは1700。
（３）
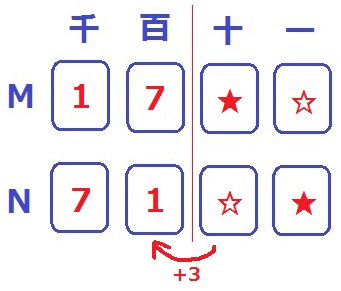
繰り上がりが３だから、４×８＝32か４×９＝36。
すなわち、★は８か９のみ。
★＝９だとＮの一の位が９となるが、４の倍数は偶数なのでありえない。
★＝８で試すと、☆＝２となる。
したがって、Ｍは1782。
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント