2024年度　埼玉県公立高校入試問題・学校選択過去問【数学】解説

平均50.2点（前年比；－0.3点）
問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
（－６ｘｙ³）÷（３/２ｘ²ｙ）×（－５ｘ）²
＝（－６ｘｙ³）÷（３/２ｘ²ｙ）×25ｘ²
＝－100ｘｙ²

（２）
対称式。
ｘｙ＝（√２＋１）（√２－１）＝（√２）²－１²＝１
ｘ＋ｙ＝（√２＋１）＋（√２－１）＝２√２

ｘｙ－ｘ－ｙ＋１
＝ｘｙ－（ｘ＋ｙ）＋１
＝１－２√２＋１
＝２－２√２

（３）
５（ｘ－１）²＋３（ｘ－１）－１＝０　←Ｘ＝ｘ－１とおく
５Ｘ²＋３Ｘ－１＝０
解の公式を適用、Ｘ＝（－３±√29）/10　←Ｘ＝ｘ－１に戻す
ｘ－１＝（－３±√29）/10
ｘ＝（７±√29）/10

（４）
共通問題と同じ。
ア：20人の中央値は10番目と11番目の平均。12～16冊の階級に含まれる。×
イ：８～12冊の度数が４。相対度数は、４/20＝0.20×
ウ：最頻値（モード）は最も現れている値で、12～16冊の階級値である14。×
エ：累積相対度数は、その階級以下の相対度数の合計。
【12～16冊の累積相対度数＝１－16～20冊の相対度数】
16～20冊の相対度数は、３/20＝0.15
12～16冊の累積相対度数は、１－0.15＝0.85〇
エ

（５）
共通問題と同じ。

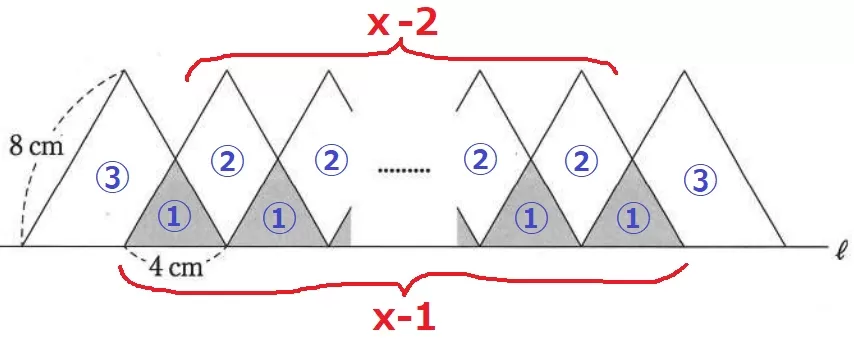
影１つの面積は正三角形の１/４。
影１つを①とすると、上図のようになる。

白…両サイドが③、あいだのｘ－２個が②→③×２＋②×（ｘ－２）＝２ｘ＋２
影…あいだのｘ－１個が①ずつ→ｘ－１
２ｘ＋２：ｘ－１＝５：２
内項と外項の積より、５（ｘ－１）＝２（２ｘ＋２）
５ｘ－５＝４ｘ＋４
ｘ＝９

（６）

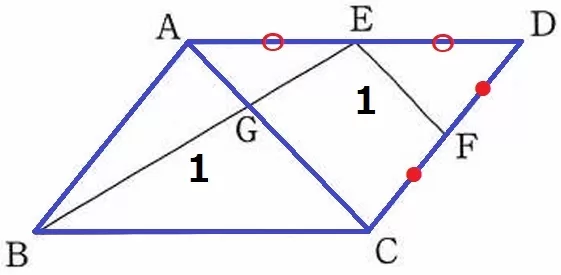
平行四辺形を対角線ＡＣで分けて２等分する。
△ＡＢＣ、△ＣＤＡの面積をそれぞれ１とする。
 
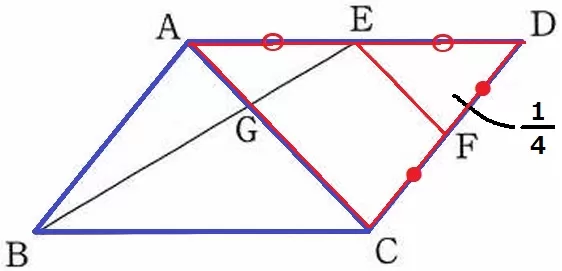
ＥとＦは中点だから、△ＤＥＦ∽△ＤＡＣの相似比は１：２。
面積比は２乗して１：４→△ＤＥＦの面積は１/４。

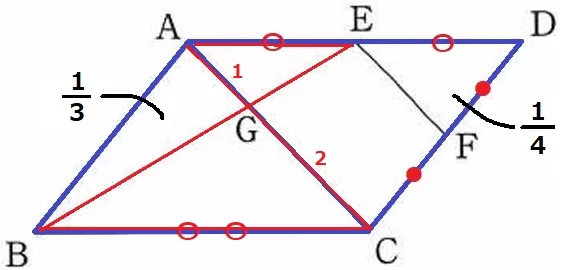
△ＡＥＧ∽△ＣＢＧより、ＡＧ：ＧＣ＝１：２
△ＡＢＧの面積は、１×１/３＝１/３
△ＡＢＧ：△ＤＥＦ＝１/３：１/４=４：３
△ＡＢＧの面積は△ＤＥＦの４/３倍。

（７）

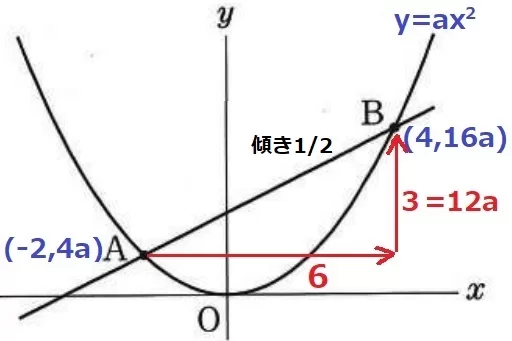
Ａ（－２、４ａ）Ｂ（４、16ａ）
ＡＢの傾きは１/２だから、Ａ→Ｂは右に６、上に３。
ＡとＢのｙ座標の差より、12ａ＝３
ａ＝１/４

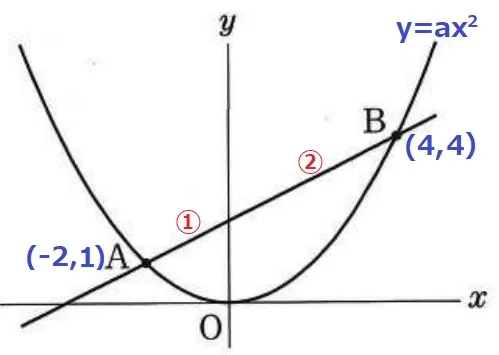
Ａ（－２、１）Ｂ（４、４）
ｘ座標の差から切片との距離は、２：４＝①：②
ｙ座標の差３＝③→①＝１
切片は１＋１＝２
ｙ＝１/２ｘ＋２

（８）

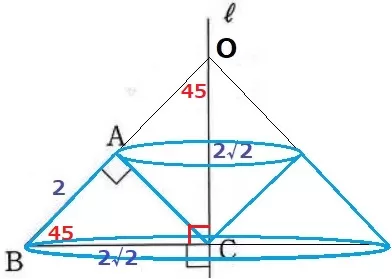
回転体はこのような図形になる。
△ＡＢＣは直角二等辺→辺の比は１：１：√２だからＢＣ＝２√２ｃｍ
円錐の頂点をＯとすると、△ＯＢＣも直角二等辺だからＯＣ＝２√２ｃｍ

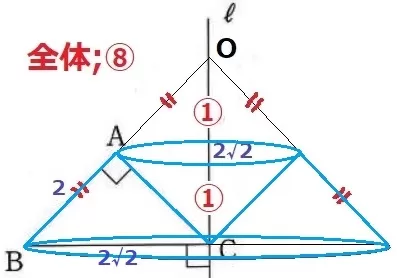
上の小さい三角錐の体積を①とすると、大きい三角錐は２×２×２＝⑧
回転体の中央の空洞部分は、小さい円錐と底面積と高さが一緒だから合同（①）。
回転体の体積は、⑧－①×２＝⑥
２√２×２√２×π×２√２÷３×⑥/⑧＝４√２πｃｍ³

＠余談＠
回転体の体積には面白い定理がある。

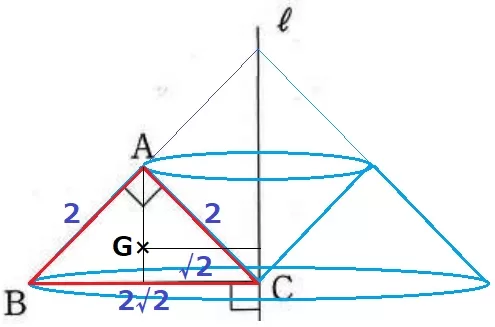
【パップス・ギュルダンの定理；回転体の体積＝断面積×重心の移動距離】
断面積は△ＡＢＣ。重心ＧはＡの真下にあり、軸との距離は√２ｃｍである。
（２×２÷２）×（√２×２×π）＝４√２πｃｍ³

（９）
共通問題の図形から線分が３本消されている。

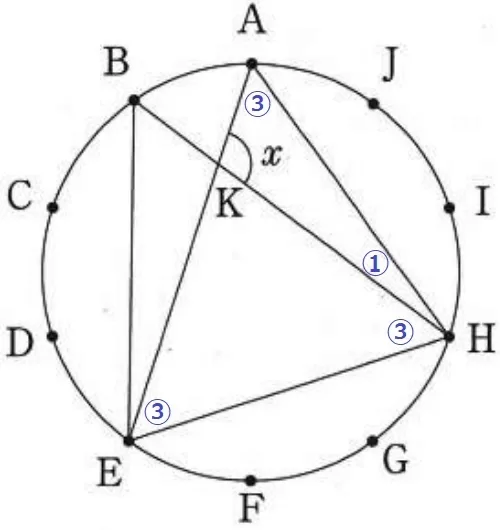
ＢＥ・ＥＨ・ＨＡに補助線。
円周角の大きさは弧の長さに比例する。
弧ＡＢは弧１つ分。∠ＡＨＢ＝①とすると、
弧３つ分（弧ＢＥ＝弧ＥＨ＝弧ＨＡ）に対する円周角である、
∠ＢＨＥ＝∠ＥＡＨ＝∠ＨＥＡ＝③

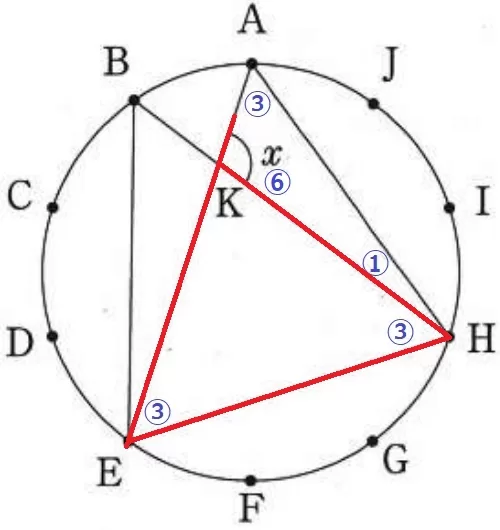
△ＫＥＨで外角定理→ｘ＝③＋③＝⑥
△ＡＢＨの内角より⑩＝180°だから、ｘ＝180×⑥/⑩＝108°

（10）
共通問題と同じ。

最小値と最大値は同じなのに、期間①より期間②の方が開花日が早い理由を記述する。
端的に『第１四分位数（Q1）と第３四分位数（Q3）がともに期間②の方が早い』で良い。
箱の区間は全データの真ん中に集まる約50％で、全体的に期間②の方が早い。

大問２（平面図形）

（１）

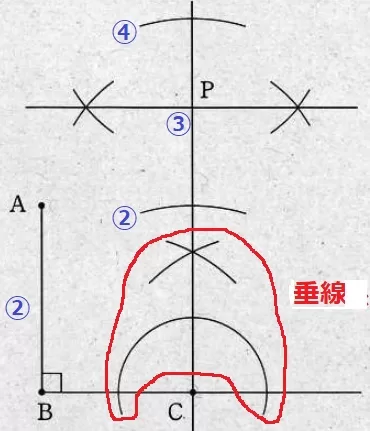
ＡＢ//ＰＣ、∠ＡＢＣ＝90°から、ＰはＣを通る垂線上にある。
ＡＢ：ＰＣ＝②：③→ＡＢ＝②の長さをＣから移し、さらに②を垂線上に移す。
Ｃからの距離②と④の垂直二等分線から、ＣＰ＝③をつくる。
【１】Ｃを通る垂線。
【２】ＣからＡＢの長さ（②）を移し、さらに真上に②を移す。
【３】②と④を垂直二等分線で割る。交点がＰ。

（２）
∠ＣＩＨ＝90°の証明。

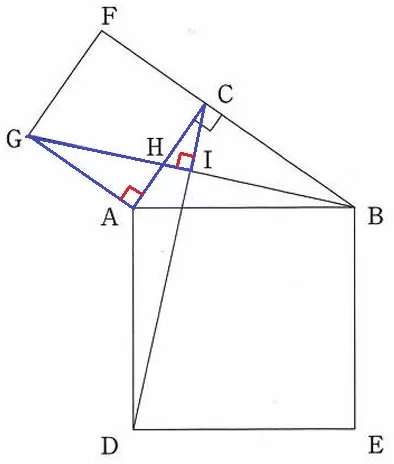
Ｃは小さい正方形の頂点。
しかし、ＨとＩは位置が不明で、△ＩＣＨの情報が足りない。
正方形の内角である∠ＧＡＨ＝90°から、隣にある△ＡＧＨとの相似を指摘すれば、
対応する角から∠ＣＩＨ=90°が導ける。
対頂角の他にもう１つの等角、∠ＡＧＨ＝∠ＩＣＨが欲しい。

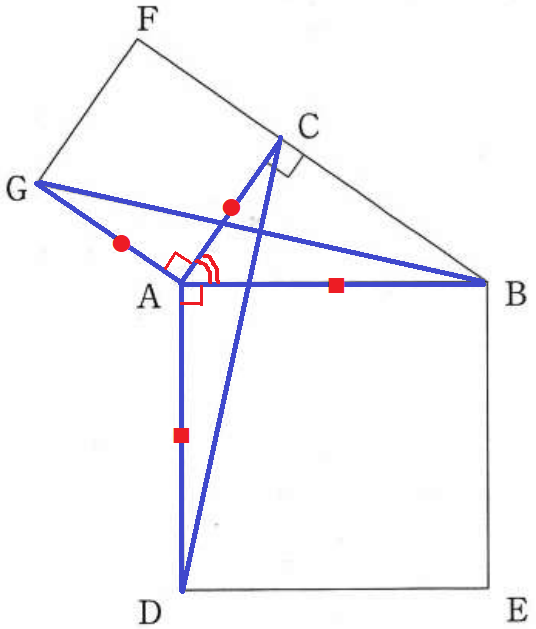
そこで、△ＡＣＤと△ＡＧＢに着目する
正方形の辺からＡＣ＝ＡＧ、ＡＤ＝ＡＢ
∠ＣＡＢ＝∠ＣＡＢ＋90°＝∠ＧＡＢ
２辺とあいだの角が等しいので△ＡＣＤ≡△ＡＧＢ

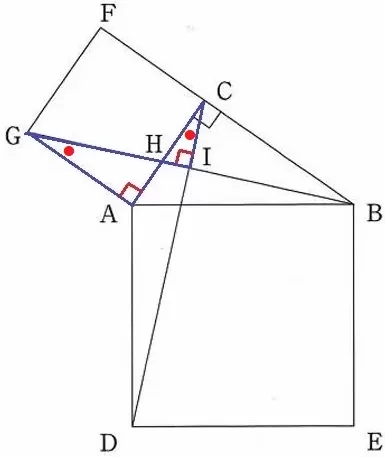
対応する角で、∠ＡＧＨ＝∠ＩＣＨ
対頂角で、∠ＧＨＡ＝∠ＣＨＩ
２角相等により△ＡＧＨ∽△ＩＣＨだから、∠ＧＡＨ＝∠ＣＩＨ＝90°

大問３（関数）

共通問題と同じ。
（１）
ｙ＝ｘにｘ＝ｔを代入→Ｑのｙ座標はｔ
ｙ＝１/３ｘ²にｘ＝ｔを代入→Ｒのｙ座標は１/３ｔ²
ア…ｔ、イ…１/３ｔ²

（２）

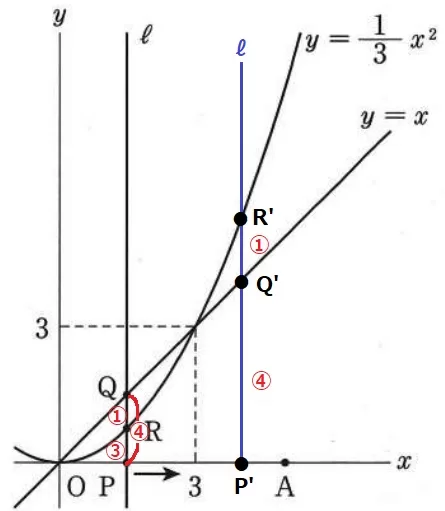
０＜ｔ＜３のときは上から順にＱ・Ｒ・Ｐだが、
３＜ｔ≦５のときはＲ・Ｑ・Ｐになる。
つまり、３を過ぎるとＱとＲが逆転してＰＲが最も長くなるので、
ＰＱ：ＰＲ＝４：３は成り立たない。
『Ｒのｙ座標がＱのｙ座標より大きくなるから』

（３）

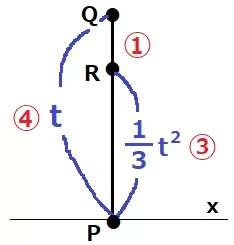
０＜ｔ＜３の場合、ｔ：１/３ｔ²＝４：３
内項と外項の積で、４/３ｔ²＝３ｔ
４ｔ²＝９ｔ
４ｔ²－９ｔ
＝ｔ（４ｔ－９）＝０
０＜ｔ＜３より、ｔ＝９/４

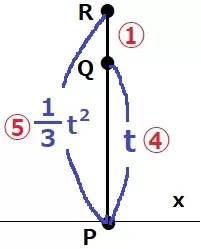
３＜ｔ≦５の場合、ｔ：１/３ｔ²＝４：５
内項と外項の積で、４/３ｔ²＝５ｔ
４ｔ²＝15ｔ
４ｔ²－15ｔ
ｔ（４ｔ－15）＝０
３＜ｔ≦５より、ｔ＝15/４
ｘ＝９/４、15/４

大問４（場合の数）

（１）
全体は２²＝４通り
２回投げてＡに止まる→２回で４マス進むのは〔表・表〕しかない。
確率は１/４。

（２）①
４マス進む組み合わせで場合分けをする。
〔表・表〕→１通り
〔表・裏・裏〕→３回のうち表をどこで出すかで３通り。
〔裏・裏・裏・裏〕→１通り
計５通り。

②

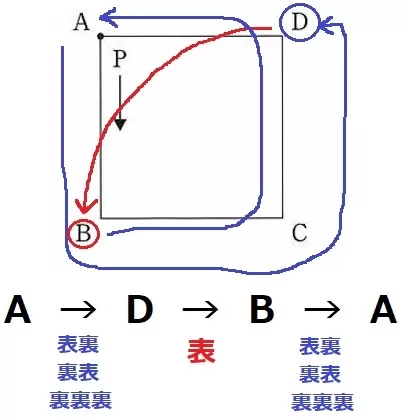
留意点は、『１周目でＡに止まらないこと』！
１回でもＡに止まると操作終了になるので２周できない。
いったんＤで止まり、表を出してＡをスキップ。ＢからＡを目指す。

Ａ→Ｄは〔表裏〕〔裏表〕〔裏×３〕の３通り。
Ｂ→Ａも同様に３通り。
３×３＝９通り

大問５（空間図形）

（１）
共通問題と同じ。

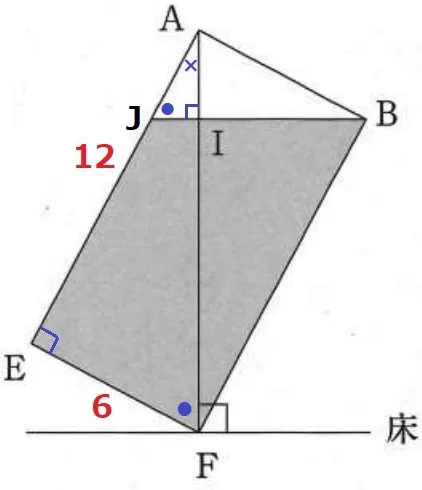
△ＡＥＦの内角において、∠ＡＦＥ＝●、∠ＦＡＥ＝×とする。
●＋×＝90°で、内角が●―×―90°であれば、ＡＥ：ＥＦ＝２：１の比が使える。
水面の左端をＪとする。
ＡＦ⊥ＪＢだから∠ＡＩＪ＝90°→△ＡＪＩにおいて、∠ＡＪＩ＝●

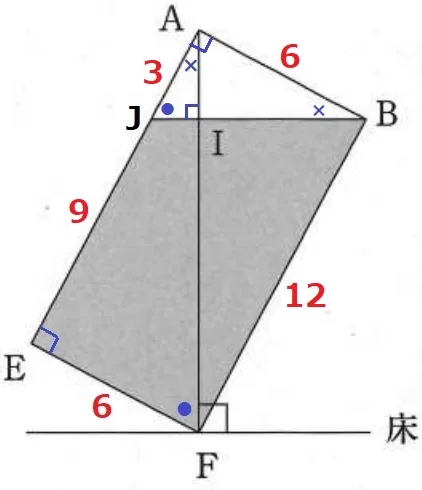
∠ＪＡＢ＝90°
△ＢＡＪは内角が●―×―90°なので、ＢＡ：ＡＪ＝２：１
ＡＪ＝６÷２＝３ｃｍ
ＥＪ＝12－３＝９ｃｍ
水の体積は、（９＋12）×６÷２×６＝378ｃｍ³

（２）

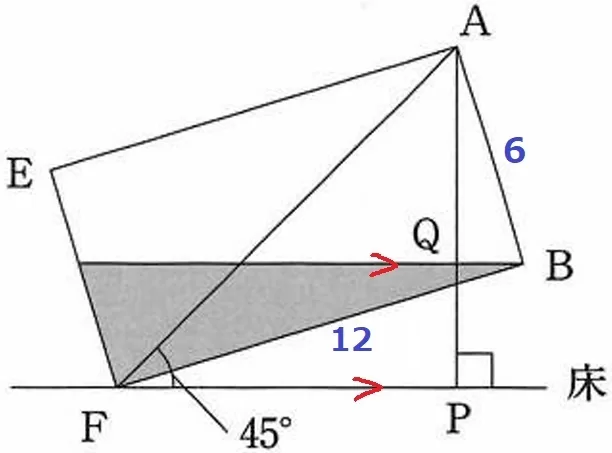
長方形の縦６ｃｍ、横12ｃｍしかわかっていない(´ﾟдﾟ｀)
しかし、平行線と直角を利用すると、いろいろな相似が見える。
12と６が対応する関係で、ＢＦは斜辺しかなさそうだから、
ＡＢを斜辺とする△ＡＢＱに着目してみる。

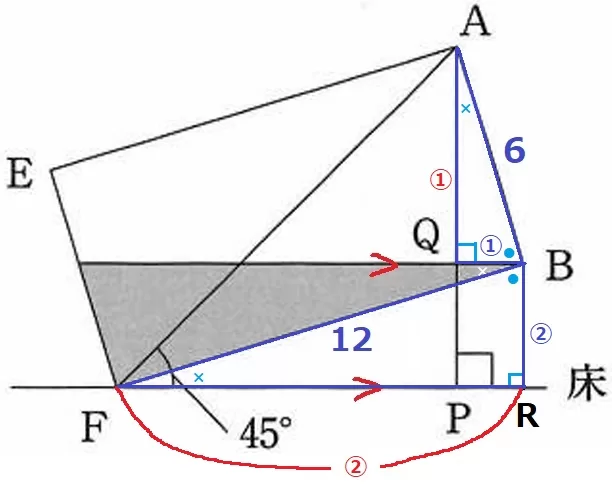
Ｂから垂線をおろし、足をＲとする。
●＋×＝90°で、∠ＡＢＦ＝∠ＱＢＲ＝90°を使って等角を移動していくと、
２角相等から△ＡＢＱ∽△ＦＢＲ
対応する辺からＡＱ：ＦＲ＝①：②、ＢＱ：ＢＲ＝①：②とする。

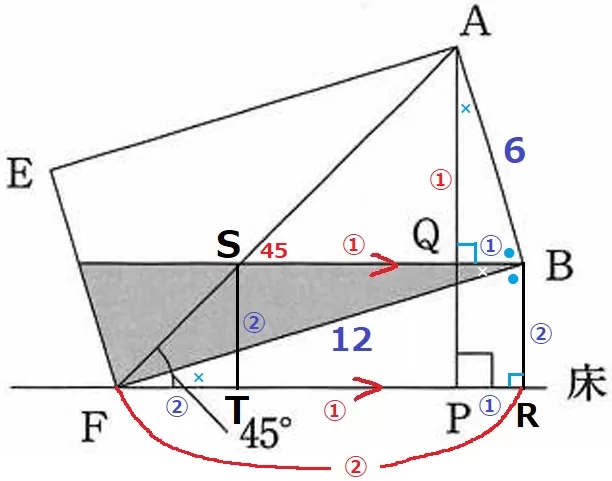
ＡＦと水面の交点をＳとし、Ｓからの垂線の足をＴとする。
同位角でＡＳＱ＝45°
△ＡＳＱは直角二等辺→ＡＱ＝ＳＱ＝ＴＰ＝①
△ＳＦＴも直角二等辺→ＢＲ＝ＳＴ＝ＦＴ＝②
ＦＲに注目すると、②＋①＋①＝②
①＝③

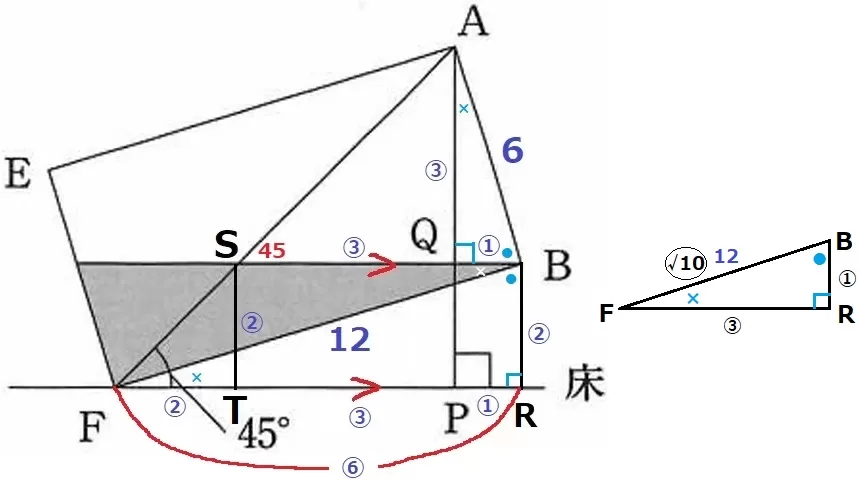
赤を３倍して青に比を統一するとこうなる。
△ＦＢＲの辺の比はＢＲ：ＦＲ＝①：③→三平方でＢＦ＝〇√10
水面の高さＢＲ＝12×①/〇√10＝６√10/５ｃｍ

＠別解＠
なんとか前問を利用できないかと試行錯誤してみました。

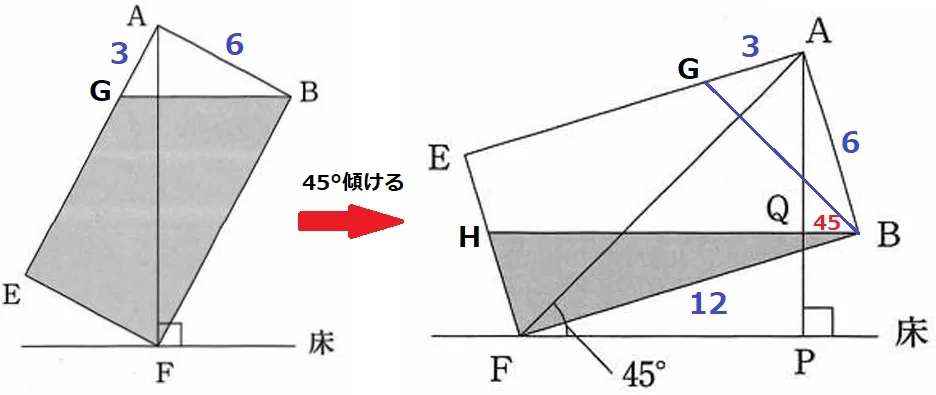
（１）はＡＦが床に対して垂直だった。そこからさらに45°傾ける。
はじめの水面の反対側をＧ、傾けた後をＨとすると、水面の傾きである∠ＧＢＨ＝45°がいえる。

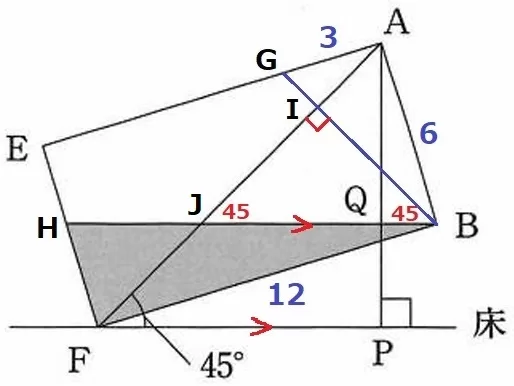
ＡＦとＢＧ、ＢＨとの交点をＩ・Ｊとする。
同位角より、∠ＩＪＢ＝45°
△ＩＪＢは直角二等辺三角形である。

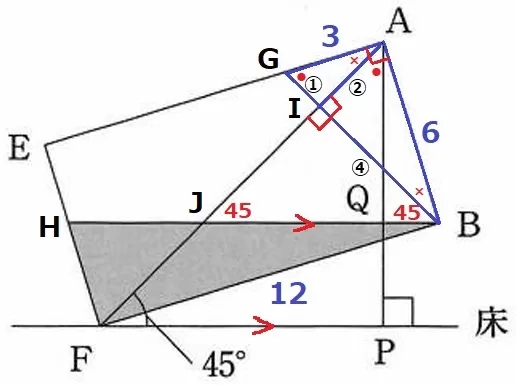
ＡＩ⊥ＢＧから●＋×＝90°を使うと、△ＡＢＧ∽△ＩＡＧ∽△ＩＢＡがいえる。
ＧＩ＝①とすると、ＡＩ＝①×２＝②、ＢＩ＝②×２＝④

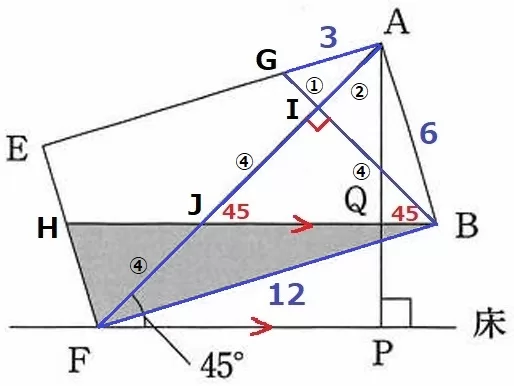
△ＡＧＩ∽ＦＢＩより、ＩＦ＝②×４＝⑧
△ＩＪＢは直角二等辺だからＩＪ＝④→ＪＦ＝④

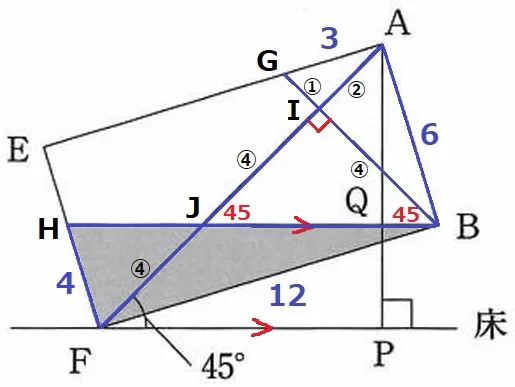
△ＡＢＪ∽△ＦＨＪより、ＨＦ＝４ｃｍ
あとはＦから垂線を引いて辺の比が１：３：√10の直角三角形をつくるか、
三平方からＢＨ＝４√10ｃｍと求め、△ＨＦＢの面積より、４×12÷４√10＝６√10/５と出ます。
この図形の別の見方ということでお納め下さい。