2023年度　京都府高校入試問題過去問・前期【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合）

（１）
－３²×｛７－（－４）²｝
＝－９×（７－16）
＝－９×（－９）
＝81

（２）
（３ｘ－２ｙ）/６－（４ｘ－ｙ）/８
＝｛４（３ｘ－２ｙ）－３（４ｘ－ｙ）｝/24
＝（12ｘ－８ｙ－12ｘ＋３ｙ）/24
＝－５/24ｙ

（３）
３√50－√２－√54÷√３　←根号同士で割算
＝15√２－√２－√18
＝14√２－３√２
＝11√２

（４）
２ｘ－３ｙ＝５　…①
３ｘ－（４ｘ－６ｙ）＝－１
－ｘ＋６ｙ＝－１
ｘ＝６ｙ＋１　…②

②を①に代入。
２（６ｙ＋１）－３ｙ＝５
９ｙ＝３
ｙ＝１/３
②に代入して、ｘ＝６×１/３＋１＝３
ｘ＝３、ｙ＝１/３

（５）
ｙ＝ａｘ²においてｘの値がｐ→ｑまで増加したときの変化の割合はａ（ｐ＋ｑ）。
－２（ａ＋ａ＋２）＝－40　←両辺を÷－２
２ａ＋２＝20
ａ＝９

（６）
（２ｘ＋ｙ＋５）（２ｘ＋ｙ－５）　←２ｘ＋ｙ＝Ｘとおいてみると…
＝（Ｘ＋５）（Ｘ－５）
＝Ｘ²－25　←Ｘを２ｘ＋ｙに戻す
＝（２ｘ＋ｙ）²－25
＝４ｘ²＋４ｘｙ＋ｙ²－25

（７）
６ｘ²＋２ｘ－１＝０
解の公式を用いる。ｘの係数が偶数だからｂ＝２ｂ’が使える。
ｘ＝（－１±√７）/６

（８）

正五角形の内角はおさえておきたい。∠ＥＤＨ＝108°
ＥＨに補助線。
△ＤＥＨは二等辺で、その底角は（180－108）÷２＝36°
∠ＥＨＧ＝108－36＝72°

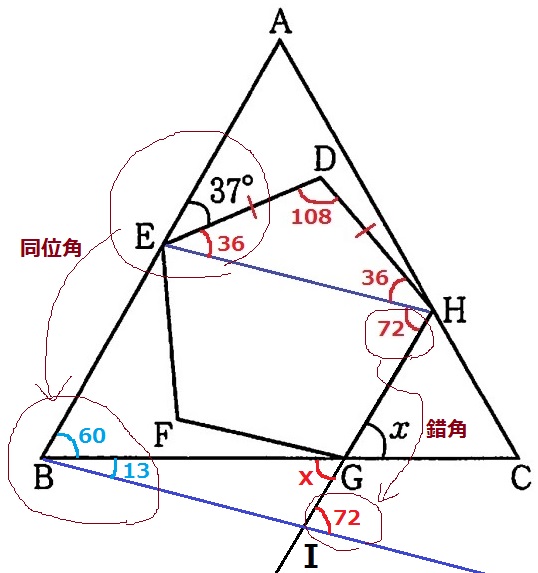
Ｂを通るＥＨに平行な線をひき、ＨＧの延長線との交点をＩとする。
ｘを対頂角、72°を錯角で移動。
同位角で、∠ＡＥＨ＝∠ＥＢＩ
∠ＧＢＩ＝（37＋36）－60＝13°
最後に△ＧＢＩで外角定理を使う。ｘ＝72－13＝59°

（９）
太郎と次郎が２人でハズレを引けば、自動的に花子だけが当たる。
太郎のハズレは４本中２本。
次郎のハズレは残り３本中１本。
２/４×１/３＝１/６

大問２（データの活用）

（１）
生徒９人が拾った合計の本数は、９×８＝72本
ａ＋ｂ＝72－（３＋９＋15＋６＋11＋８＋４）＝72－56＝16本
０＜ａ＜ｂの条件から、ａ＋ｂ＝１＋15＝２＋14＝３＋13＝４＋12…＝７＋９
この７通りのうち、本数がかぶらない組み合わせは２＋14しかない。
ａ＝２、ｂ＝14

（２）

値を昇順に並べる。
10人のQ2（第２四分位数；中央値）は５番目と６番目の平均。
Q1（第１四分位数）は下位５つの真ん中で下から３番目。
Q3（第３四分位数）は上位５つの真ん中で上から３番目。
先生がどこにくるかは不明だが、このあたりがＱ１かＱ３になる。

３、４が連続している点に着目する。
もし、先生が３以下ならばQ1は３、先生が４以上でならばQ1は４。この２通りに絞られる。
四分位範囲＝Ｑ３－Ｑ１＝９
Ｑ1が３のとき、Ｑ3は12になるが、先生は３本以下なので12は無い。×
Ｑ3が４のとき、Ｑ3は13になり、先生が13本であれば成り立つ。〇
したがって、先生は13本。

大問３（空間図形）

（１）

正八面体の特徴を知っておかないと、時間が間に合わないと思う(;´･ω･)
立方体の各面の中心を結ぶと正八面体になる。
この特徴を抑えておくと、いろんなところにある等辺や直角が見えやすい。

ＢＤとＣＥの交点をＯとする。
立方体のどの面から見てもＯは中心にある→Ｏは立方体の中心。
立方体の１辺は４ｃｍ。
△ＯＢＣは等辺２ｃｍの直角二等辺三角形。
１：１：√２より、正八面体の１辺ＢＣ＝２√２ｃｍ

（２）

ＢＤの中点は前図のＯ。ＯをＨに変えた。
三角錐Ｆ―ＢＨＥは正八面体の８分の１にあたる。
２×２÷２×２÷３＝４/３ｃｍ³

（３）

Ａは立方体の中心の真上にある。
求めたいのはＡと面ＢＦＣとの距離だが、
対称性からＡと面ＢＦＥ、面ＥＦＤ、面ＣＦＤとの距離と等しい。
アングルの都合上、Ａと面ＢＦＥとの距離を求める。

Ｆを１階、ＢとＥを２階、Ａを３階とする。
ＦＢとＦＥの延長線上で、Ａと同じ３階にある点をそれぞれＩ、Ｊとする。
Ｉ、Ｊの中点Ｋの位置を真上から見た図で調べると、Ｋは立方体の頂点にある。
（△ＦＥＢと△ＦＪＩは相似比が１：２）

ＫＡは等辺２ｃｍの直角二等辺の斜辺→ＫＡ＝２√２ｃｍ
直角三角形ＡＫＦで切り取る。Ａから垂線をひき、足をＬとする。
 
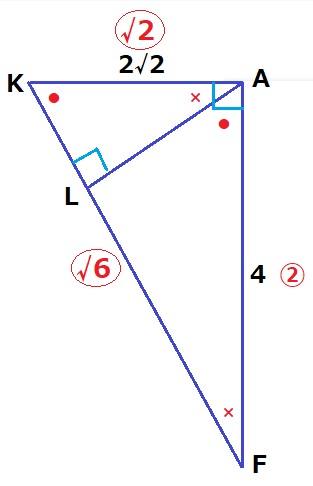
●＋×＝90°から２角相等で、△ＡＫＦ∽△ＬＫＡ。
△ＡＫＦの辺の比で、ＫＡ：ＡＦ＝２√２：４＝√２：２
三平方の定理から、ＫＦ＝√６
△ＬＫＡの辺の比より、ＫＡ：ＬＡ＝√６：２なので、
ＡＬ＝２√２×２/√６＝４√３/３ｃｍ

大問４（関数）

（１）
反比例の比例定数ａはｘとｙの積。
Ａ座標から、ａ＝２×６＝12

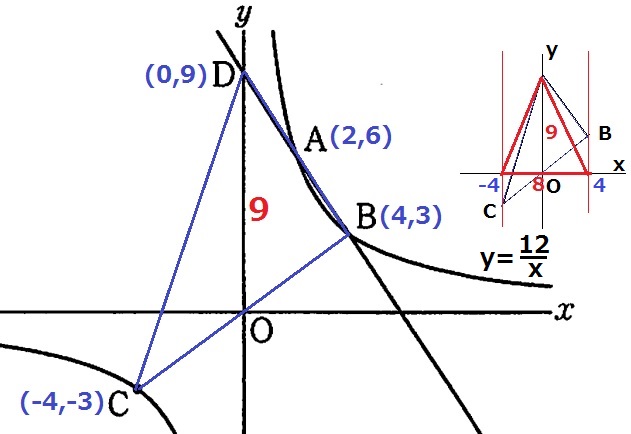
座標を確定していく。
Ｂ（４、３）から左に２、上に３移動してＡ（２、６）。
Ａからさらに左に２、上に３移動してＤ（０、９）。
Ｃ（－４、－３）
ＢとＣは原点に関して対称であり、ＢＣは原点Ｏを通過する。

△ＢＤＣを等積変形すると、底辺８、高さ９の三角形になる。
８×９÷２＝36

（２）

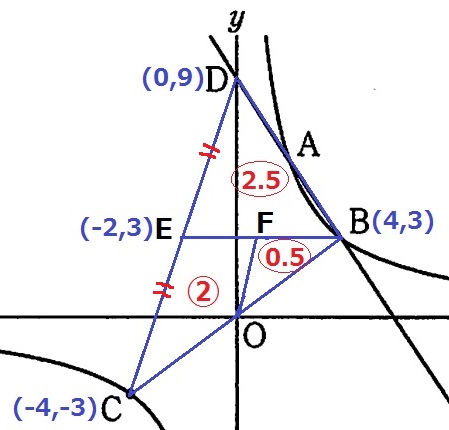
ＥＢはｘ軸に平行→Ｅのｙ座標はＢと同じ３。
これはＣとＤのｙ座標の平均なので、ＥはＣＤの中点である。Ｅ（－２、３）
△ＢＤＣの面積を⑤とおくと、ＣＥ：ＥＤ＝１：１より△ＢＥＣ＝⑤÷２＝〇2.5
仮定から四角形ＣＯＦＥ＝②、△ＢＦＯ＝〇2.5－②＝〇0.5

面積比を整理すると、△ＢＦＯ：△ＢＥＣ＝0.5：2.5＝①：⑤
これを隣辺比で表すと、ＦＢ×１：ＥＢ×２＝①：⑤
外項と内項の積で、ＦＢ×５＝ＥＢ×２
ＦＢ：ＥＢ＝２：５
ＥＢ＝６だから、ＦＢ＝６×２/５＝12/５
Ｆのｘ座標は、４－12/５＝８/５

大問５（平面図形）

（１）
△ＩＧＢ∽△ＩＦＥの証明。
折り返しによる等角の対称関係に留意する。

対頂角（×）
錯角＋ＢＤ折り返し＋ＧＨ折り返し（●）
２角相等で∽。

（２）

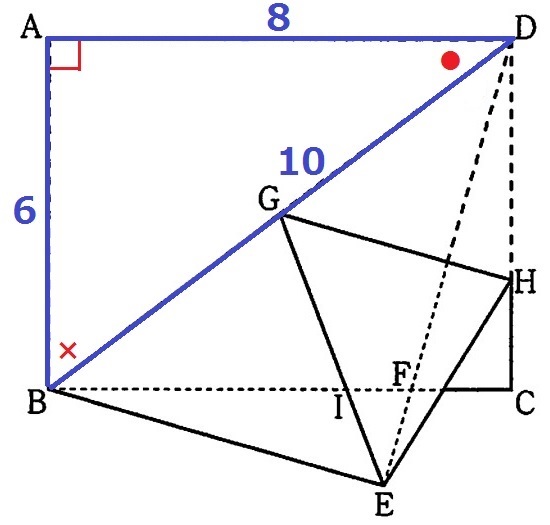
ＡＢ＝６ｃｍ、ＡＤ＝８ｃｍから直感したい。
△ＡＢＤは辺の比が３：４：５の直角三角形→ＢＤ＝10ｃｍ
内角が●―×―90°の三角形は３：４：５である。

なんとなくＧがＢＤの中点っぽい…。
折り返しで●と×を記す。
同じく折り返しで、∠ＤＡＢ＝∠ＤＥＢ＝90°
∠ＧＥＢ＝90－●＝×
△ＧＢＥは底角が等しいから二等辺三角形。
ＢＤ＝ＢＧ＋ＧＤ＝ＢＧ＋ＧＥ＝10ｃｍ
ＢＧ＝ＧＥ＝10÷２＝５ｃｍ
やはり、ＧはＢＤの中点であった。

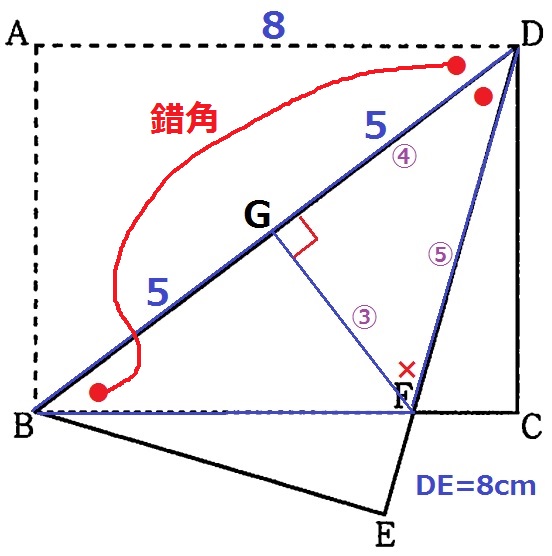
ＤＥ＝８ｃｍだから、ＤＦがわかればＦＥが求まる。
Ⅰ図に戻ると見えやすい。
錯角で∠ＤＢＦ＝●→等しい底角から△ＢＦＤは二等辺三角形。
頂角Ｆから底辺ＢＤに垂線をおろすと、その足はＢＤの中点Ｇを通過する。
△ＤＧＦの内角は●と90°だから残りの角は×。
３：４：５が使って、ＤＦ＝５×⑤/④＝25/４ｃｍ
ＥＦ＝８－25/４＝７/４ｃｍ

＠余談＠

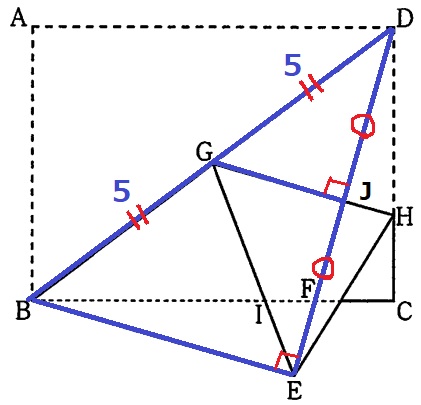
ＧがＢＤの中点である説明ですが、線対称でＧＨ⊥ＤＥ、
交点をＪとするとＪはＤＥの中点、∠ＤＪＧ＝∠ＤＥＢ＝90°、
青線の相似からＧが中点ともいえます。

（３）
本試験の最難関です(ﾉ)`ω´(ヾ)

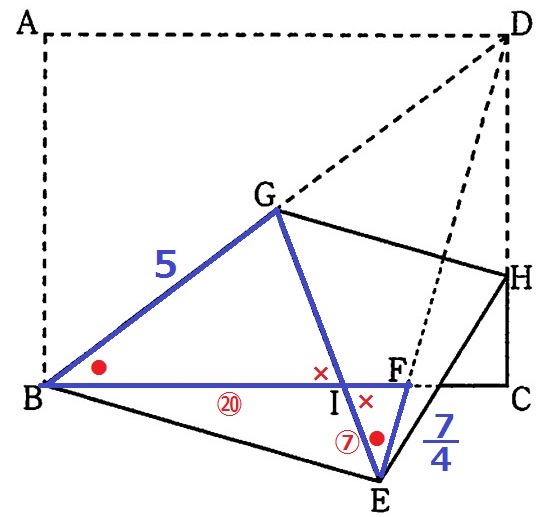
ＢＩを１辺とする相似は（１）で求めている。
ＢＩ：ＥＩ＝５：７/４＝⑳：⑦
ＧＥ＝５ｃｍ、ＧＩを〇の比で表せられないか…。

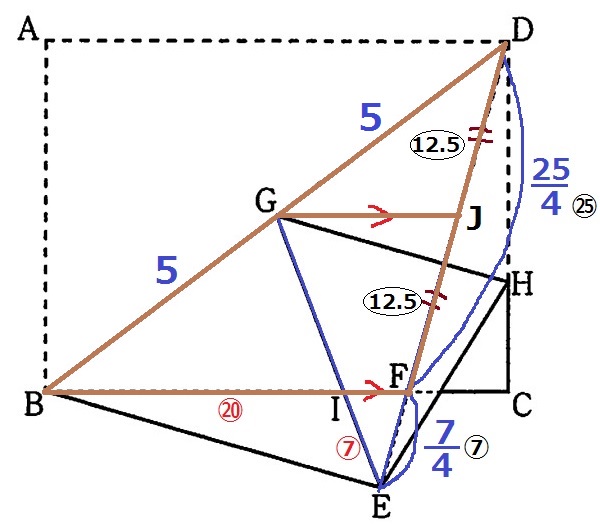
Ｇを通るＢＣに平行な線をひき、ＤＥとの交点をＪとする。
前問で使用した数字から、ＤＦ：ＦＥ＝25/４：７/４＝㉕：⑦
ＤＧ：ＧＢ＝ＤＪ：ＪＦ＝１：１
ＪＦ＝㉕÷２＝〇12.5

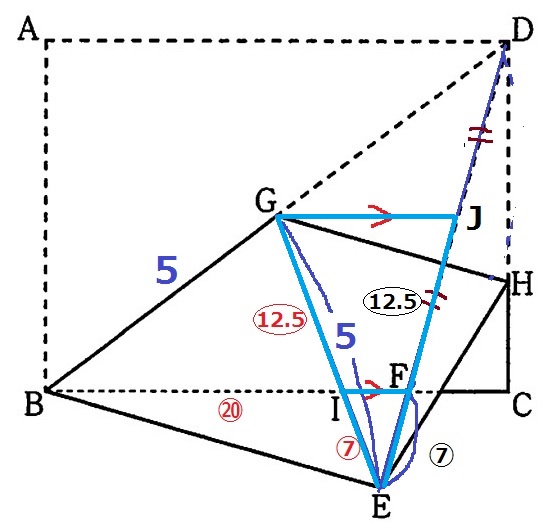
ＧＩ：ＩＥ＝ＪＦ：ＦＥより、ＧＩ＝〇12.5
ＧＥ＝５ｃｍは〇19.5に相当するので、
ＢＩ＝５×⑳/〇19.5＝200/39ｃｍ

大問６（規則）

（１）

書いて調べる。
差の差が＋８ずつ増加している。
72個

＠別解＠
よく見ると、１周目〔右１、上１、左２、下２〕２周目〔右３、上３、左４、下４〕
…と続いている。
４周目は１＋１＋２＋２＋…７＋７＋８＋８。
つまり、１～８の和を２倍すればいい。
等差数列の和の公式から、（１＋８）×８÷２×２＝72

（２）
左矢印の数をみると、【２、４、６、８…】と偶数がつづく。
すなわち、20番目の偶数40までの和を求めれば良い。
等差数列の和の公式を用いて、（２＋40）×20÷２＝420個

（３）

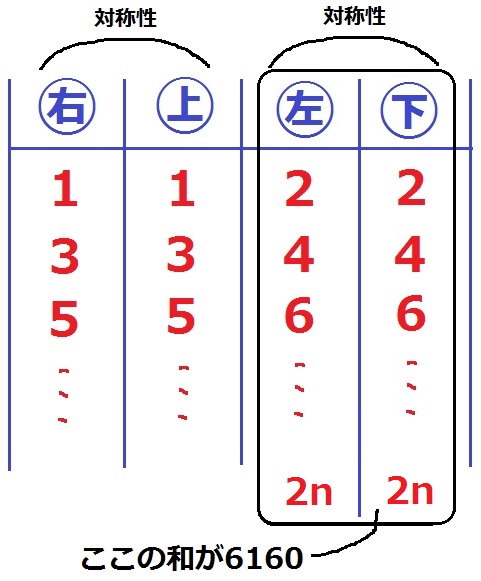
３番目まで上下左右の内訳を調べると、右と上、左と下に対称性がある。
（上＋左＋下）－右　←上と右を相殺する
＝左＋下＝6160
左と下の和が6160になる。

もっと分解すると、下＝6160÷２＝3080
最後をｎ番目とすると下の和は、
２＋４＋６＋…２ｎ
＝２（１＋２＋３＋…ｎ）＝3080　←両辺÷２
１＋２＋３＋…ｎ＝1540
すなわち、１からｎ番目の連続する整数和が1540となるｎを求めればいい。
１/２ｎ（ｎ＋１）＝1540
ｎ（ｎ＋１）＝3080

50²＝2500、60²＝3600
ｎは50～60の範囲にあり、１の位が０なので素因数５が必要→ｎかｎ＋１が55。
54×55＝2970、55×56＝55×（54＋２）＝2970＋110＝3080！
（もしくは、3080÷７が割り切れるので７の素因数を含む56→55×56）
ｎ＝55