問題はコチラ→ＰＤＦファイル
大問１（小問集合）
（１）
７＋３×（－４）
＝７－12
＝－５
（２）
５（２ａ＋ｂ）－（３ａ－ｂ）
＝10ａ＋５ｂ－３ａ＋ｂ
＝７ａ＋６ｂ
（３）
√18＋14/√２
＝３√２＋７√２
＝10√２
（４）
反比例はｘとｙの積が比例定数ａで一定。
ｙ＝－４×３÷６＝－２
（５）
ｘ（ｘ＋７）＝８（ｘ＋９）
ｘ2＋７ｘ＝８ｘ＋72
ｘ2－ｘ－72
＝（ｘ＋８）（ｘ－９）＝０
ｘ＝－８、９
（６）
23÷65＝0.353…≒0.35
（７）
ｙ＝－１/２ｘ2のグラフを描く。
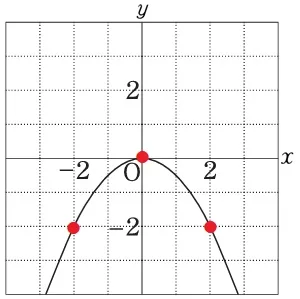
ａ＜０なので、上に凸のグラフ。
通過すべき格子点は原点Ｏ・（－２、－２）・（２、－２）の３点。
（８）
13人の中央値は７番目の値。
第３四分位数は上位６人の真ん中、上から３番目と４番目の平均。
53と56の平均→差の３÷２＝1.5だから54.5個。
（９）
60人中45人が興味アリ。この割合は母集団も同じとみなす。
全体は560人だから、560×45/60＝420人
大問２（確率）
（１）
余事象。
【少なくとも１個は白＝全体－２回とも赤】
全体は４×４＝16通り、２回とも赤は１通り。
少なくとも１個は白である確率は、１－１/16＝15/16
（２）
順番の違いで確率が変動しない理由を、樹形図か表を使って説明する。
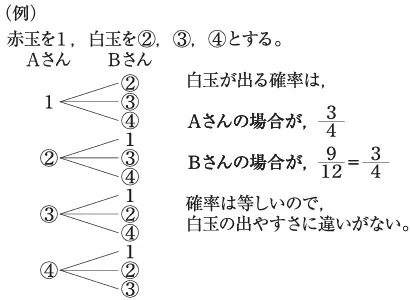
公式解答より。
白を出す確率は左のＡが３/４、右のＢが９/12＝３/４で変わらない。
＠余談＠
数学の世界ではモンティ・ホール問題という確率にまつわる有名なトピックがあります。
高校数学の美しい物語より。
結論をいうと、扉を変えた方が正解の確率は上がります。
詳細はリンク先を読んでください。高校数学では”条件付き確率”で扱います。
『新情報を得ると、確率は変動する可能性がある』という点はおさえておきましょう。
大問３（整数）
（１）
ｎ＋（ｎ＋１）＋（ｎ＋２）
＝３ｎ＋３
＝３（ｎ＋１）
ｎ＋１が整数だから、３（ｎ＋１）は３の倍数。
（２）
（ｎ＋１）（ｎ＋２）－ｎ（ｎ＋１）
＝ｎ2＋３ｎ＋２－ｎ2－ｎ
＝２ｎ＋２
＝２（ｎ＋１）
真ん中の数ｎ＋１を２倍した数になる。
さらに、２ｎ＋２＝ｎ＋（ｎ＋２）に変形すると、最も小さい数と最も大きい数の和になる。
Ａ…２（ｎ＋１）、Ｂ…ウ
（３）
最も小さい数をｍとすると、連続する３つの整数はｍ、ｍ＋１、ｍ＋２となる。
（ｍ＋１）2－１
＝ｍ2＋２ｍ＋１－１
＝ｍ（ｍ＋２）
したがって、連続する３つの整数のうち、真ん中の数の２乗から１をひいた差は、
最も小さい数と最も大きい数の積になる。
（４）
連続する４つの整数をｎ、ｎ＋１、ｎ＋２、ｎ＋３とする。
Ｘ＝ｎ＋（ｎ＋１）＝２ｎ＋１
Ｙ＝（ｎ＋２）＋（ｎ＋３）＝２ｎ＋５
ＸＹ
＝（２ｎ＋１）（２ｎ＋５）
＝４ｎ2＋10ｎ＋２ｎ＋５
＝４ｎ2＋12ｎ＋５
これが何かの４の倍数にしたい→４でくくる必要がある。
前半の４ｎ2＋12ｎは４でくくれるが、５がくくれない。
そこで、５＋３＝８にして定数項も４の倍数にする。
４ｎ2＋12ｎ＋５＋３
＝４（ｎ2＋３ｎ＋２）
＝４（ｎ＋１）（ｎ＋２）
３を足すと、２番目に小さい数と２番目に大きい数の積の４倍になる。
Ｑ…３、Ｃ…ウ
大問４（数量変化）
（１）
200kWh以下なので、１kWhあたり24円。
400＋24×80＝2320円
（２）
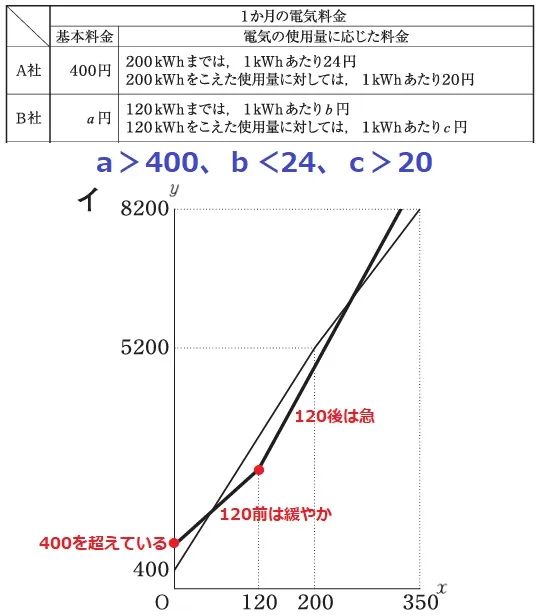
ａ＞400→基本料金（切片）は400を超える。
ｂ＜24→前半はＡより傾きが緩やか。Ａに追い越される。
ｃ＞20→後半（とくに200kWh以降）はＡより傾きが急。Ａを追い越す。
イ
（３）
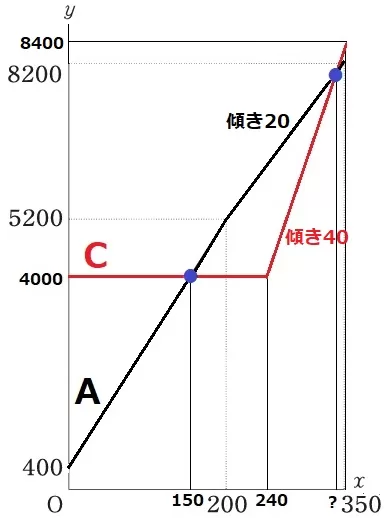
Ｃ社をグラフに追記する。
ＣがＡより安くなるのは、150kWhから再び２直線が交わる点のあいだである。
うしろの交点のｘ座標が答えである。
Ａの傾きは１kWhごとに20円なので20。
Ｃの傾きは（8400－4000）÷（350－240）＝40
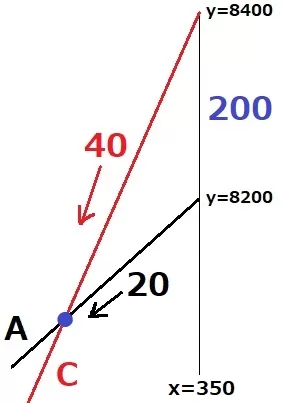
最後を取り上げる。
最終的にＡとＣの差は200円になる。ここから逆再生する。
Ａを20、Ｃを40ずつ戻していくと、１kWhごとに40－20＝20円ずつ差が縮まる。
200÷20＝10kWhで差がなくなる。
350－10＝340kWh
大問５（平面図形）
（１）
垂線の作図法の理由。
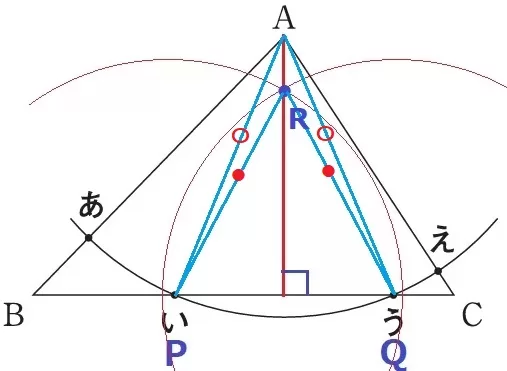
ＢＣ上の点い・うをＰ・Ｑとする。
Ｐ・Ｑからそれぞれ等しい半径の円を描き、交点をＲとする。
ＡとＲを結ぶと、ＡＲ⊥ＰＱになる。
ＡとＲはＰ・Ｑから等距離にある点で、ＡＲを対称の軸とするとＰとＱは対応する点である。
△ＡＰＲと△ＡＱＲは線対称で合同。
対応する点を結んだＰＱと対称の軸ＡＲは直交する。
点Ｐ、Ｑとする２点…い・う、図形…ア
（２）
△ＡＦＥ∽△ＢＣＥの証明。
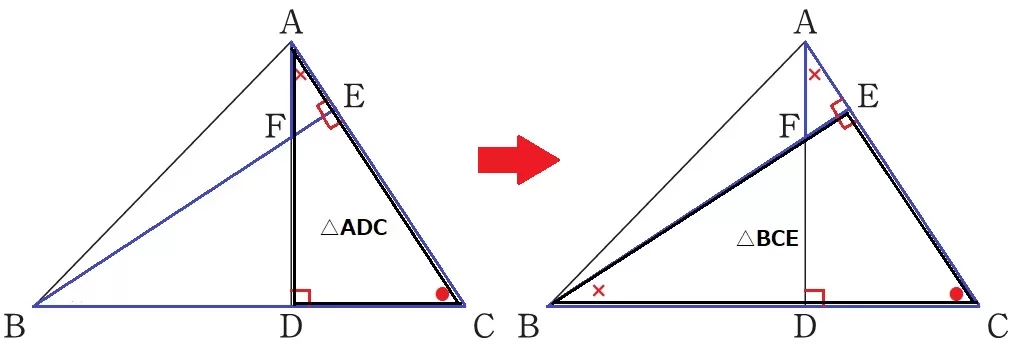
ＢＥ⊥ＡＣより、∠ＦＥＡ＝∠ＣＥＢ＝90°
もう１つの等角は直角を利用する。
∠ＥＡＦ＝×とする。
△ＡＤＣの内角である∠ＤＣＡ＝●とすると、●＋×＝90°
△ＢＣＥの内角から、∠ＥＢＣ＝90－●＝×
∠ＥＡＦ＝∠ＥＢＣ
２角が等しいので∽。
（３）
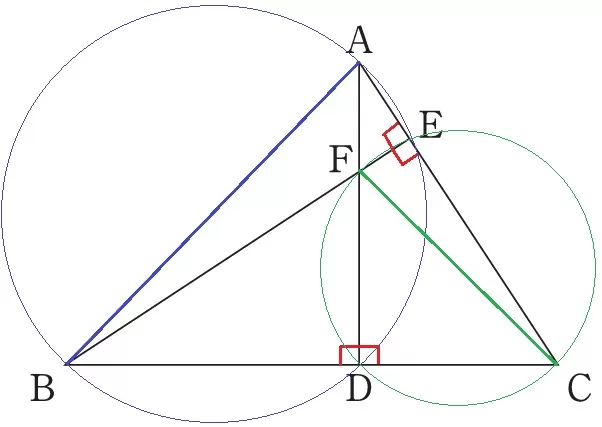
直径に対する円周角は90°
直角三角形の斜辺の中点を中心とする円を描くと、３つの頂点は同一円周上にある。
さらに、斜辺を共有する２つの直角三角形では４点が同一円周上にある。
直径をＡＢとすると、４点Ａ、Ｂ、Ｄ、Ｅが同一円周上、
直径をＣＦとすると、４点Ｃ、Ｄ、Ｅ、Ｆが同一円周上にある。
（Ａ、Ｂ、Ｄ、Ｅ）（Ｃ、Ｄ、Ｅ、Ｆ）
（４）
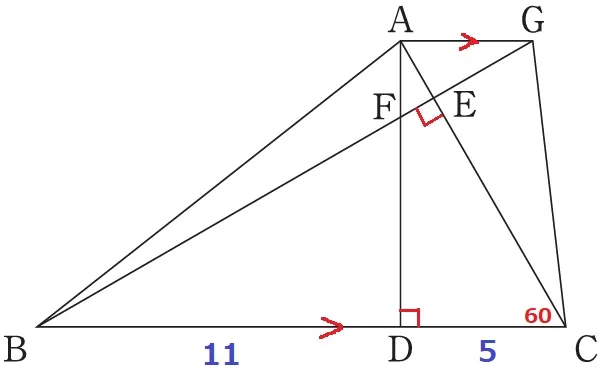
辺の情報が下に偏っているので、相似を用いて上の情報を探りに行く。
60°と90°といえば１：２：√３の有名三角形だが、なるべく無理数の√３は避けたい。
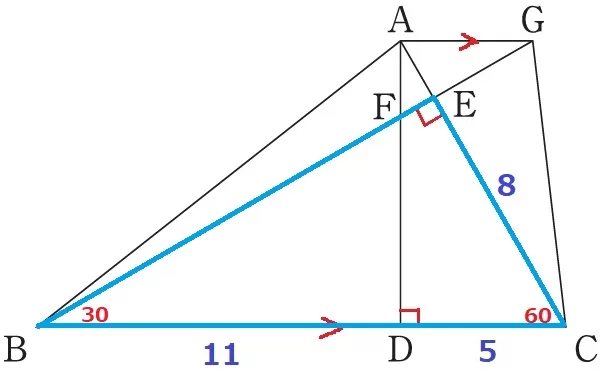
△ＢＣＥに着目。
ＢＣ：ＣＥ＝２：１だから、ＣＥ＝16÷２＝８ｃｍ
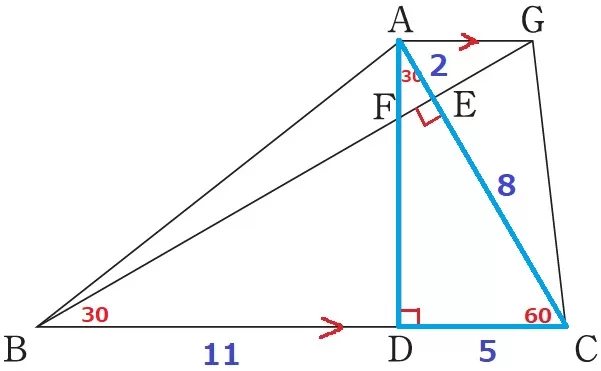
△ＡＣＤに着目。
ＡＣ：ＣＤ＝２：１だから、ＡＣ＝５×２＝10ｃｍ
ＡＥ＝10－８＝２ｃｍ
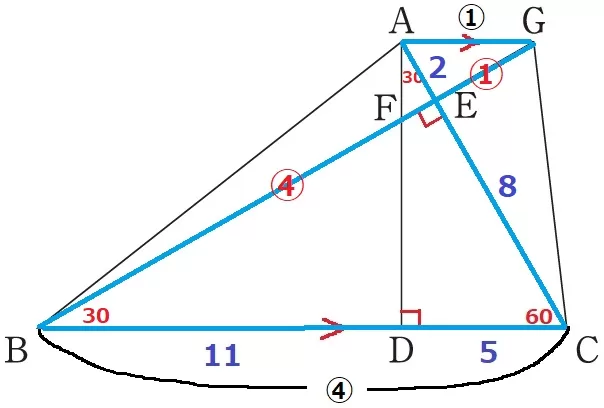
△ＡＥＧ∽△ＣＥＢより、辺の比はＡＥ：ＣＥ＝２：８＝①：④
四角形ＡＢＣＧの面積を１とする。
【方針；四角形ＡＢＣＧ→△ＡＢＧ→△ＡＢＥ】
四角形ＡＢＣＧを上底ＡＧ（①）：下底ＢＣ（④）＝△ＡＢＧ：△ＢＣＧに分ける。
△ＡＢＥの面積は、四角形ＡＢＣＧの１×①/⑤×④/⑤＝４/25倍
大問６（空間図形）
（１）
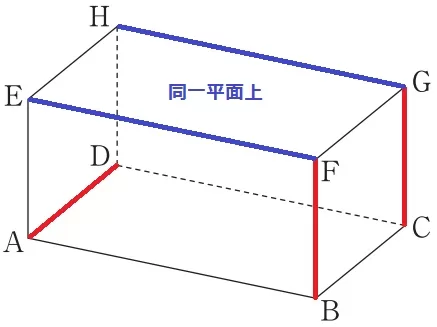
ねじれの位置→延長しても交わらない、かつ平行でもない。
ＡＤとネジレにあるのはＢＦ・ＣＧ・ＥＦ・ＨＧ。
このうち面ＥＦＧＨに垂直なのは辺ＢＦ、辺ＣＧ。
（２）
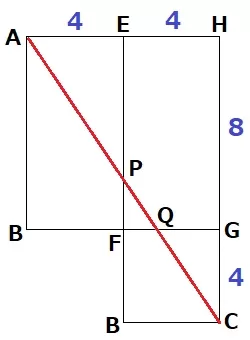
最短距離なので展開図を作成。
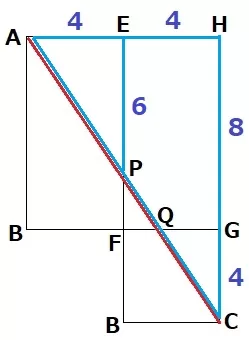
ＥはＡＨの中点。
△ＡＰＥ∽△ＡＣＨより、ＥＰ＝12÷２＝６ｃｍ
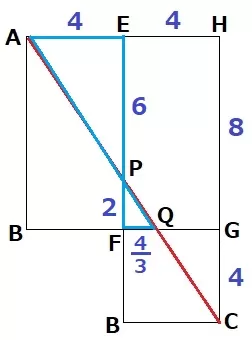
ＰＦ＝８－６＝２ｃｍ
△ＡＥＰ∽△ＱＦＰより、ＦＱ＝４×２/６＝４/３ｃｍ
△ＰＦＱで三平方→ＰＱ＝２√13/３ｃｍ
（３）
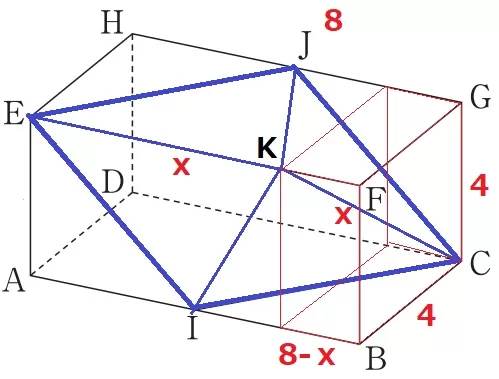
Ｋの位置を特定したい。
ＥＫ＝ＫＣ＝ｘとする。
ＫＦ＝８－ｘ
ＫＣを対角線とする直方体をつくり、対角線ＫＣで方程式を立てる。
ｘ2＝（８－ｘ）2＋４2＋４2
ｘ2＝64－16ｘ＋ｘ2＋16＋16
16ｘ＝96
ｘ＝６
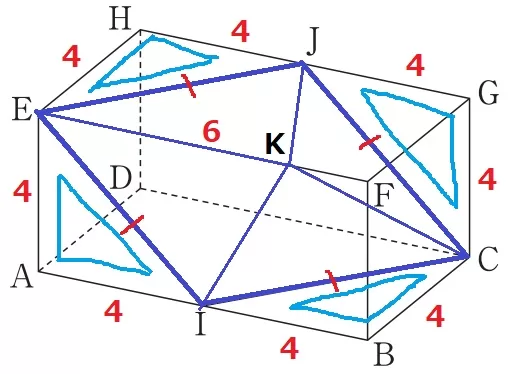
ところで、ＥＩ・ＩＣ・ＣＪ・ＪＥは等辺４ｃｍの直角二等辺の斜辺である。
四角形ＥＩＣＪは４辺が等しい菱形。
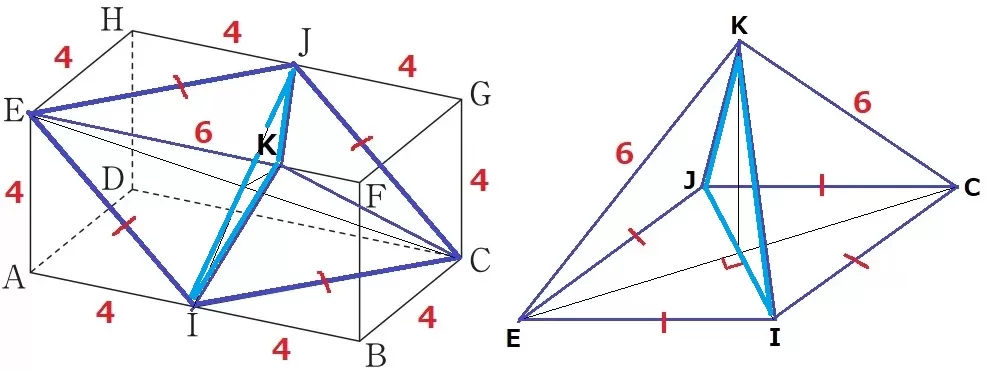
正四角錐Ｋ―ＥＩＣＪを面ＫＪＩで分割すると左右対称である。
正四角錐Ｋ―ＥＩＣＪ＝三角錐Ｋ―ＥＩＪ×２
Ｋ―ＥＩＪをＩ―ＥＫＪで捉えると、底面は△ＥＫＪ、高さは４ｃｍにあたる。
したがって、四角錐の体積は、６×４÷２×４÷３×２＝32ｃｍ3
後半の大問の後半の小問は思考力レベルが高い。
大問１
配点18点。基本レベルゆえ落としたくない。
（６）小数第２位まで求める→小数第３位を四捨五入する。
大問２
１回目に取り出した玉を戻すか戻さないかを見逃さない。
（２）白玉は区別する。それを樹形図にきちんと記す。
大問３
式の変形はサッとできるようにしたい。
（２）２ｎ＋２を２（ｎ＋１）以外の形に変える。
（４）Ｘ、Ｙをｎで表して積を計算してみる。
何かの４の倍数という結果から逆算して、不足分をＱで補う。
補った式を４でくくると、Ｃの中身がわかる。
大問４
（２）良い問題だと思う。
（３）正確なグラフを描く。計算に必要な数値はグラフ上にもある。
ｘ＝350のときの差が200。変化量の差から後ろに戻す。
大問５
（１）実際に描いてみよう。
（２）直角が多いので、●＋×＝90°を用いて三角形をうまく乗り換える。
（３）同一円周上の４点→等しい円周角を探す。（円周角の定理の逆）
（４）１：２：√３からＢＦなどを求めたくなるが、
なるべく１：２のみで上の情報を探りに行けないかを考える。
大問６
（１）ネジレにもう１つ条件が加えられた。
（２）ＰＱを斜辺とする直角三角形の他２辺を相似から求める。
（３）ＫＣが立体の内部を通る直線なので、直方体の対角線から方程式を立てる。
断面の四角形ＥＩＣＪの特徴をつかむ。
求めたい正四角錘の半分である三角錐は底面が△ＥＫＪ（もしくは△ＥＫＩ）で、
直方体の面上にある三角形だから体積が出しやすい。
公立高校入試解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント