平均61.4点(前年比;+13.6点)

問題はこちら→東京都教育委員会
大問1(小問集合)-51.6%
(1)イ 64.0%
*燃焼後に質量が大きくなった物体→スチールウール
スチールウールは鉄。鉄に酸素が結合して酸化鉄になった。
2Fe(鉄)+O2(酸素)→2FeO(酸化鉄)
一方、有機物である木片を燃焼すると二酸化炭素や水(水蒸気)が発生し、
これらが空気中に逃げて質量が軽くなる。
石灰水が白く濁った集気びん→木片を入れた集気びんP
石灰水に二酸化炭素を通すと白く濁る。
(2)ア 52.1%
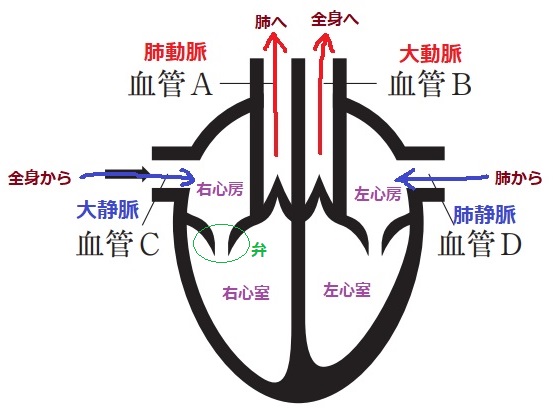
*血液の流れは、全身→大静脈(C)→右心房→右心室→肺動脈(A)→肺→肺静脈(D)→左心房→左心室→大動脈(B)→全身
右心室~(肺)~左心房を肺循環、左心室~(全身)~右心房を体循環という。
動脈は血液が心臓から出ていく血管(A・B)
静脈は血液が心臓に入ってくる血管(C・D)
弁の形から血流の向きを判断できる。
動脈血は酸素を多く含む血液。静脈血は酸素が少なく、二酸化炭素が多い血液。
肺でガス交換を受けた後の肺静脈(D)と全身に送り出される大動脈(B)に動脈血が流れる。
@酸素解離曲線@

センター試験(2010年度)より。高校生物で習う酸素解離曲線。
横軸は酸素濃度。縦軸は酸素へモグロビンの割合。
酸素ヘモグロビンとは、酸素と結合しているヘモグロビンのこと。
酸素濃度の高い動脈血は酸素ヘモグロビンが多く、鮮やかな赤色になる。
反対に、静脈血は酸素ヘモグロビンが少なく、暗い赤色をしている。
酸素濃度が低く、二酸化酸素濃度が高い各細胞の組織(酸素の需要地)では、
ヘモグロビンが酸素を離して組織に供給することで酸素ヘモグロビンの割合が低くなる。
筋肉に含まれるミオグロビンはヘモグロビンよりも酸素とよくくっつき、
ヘモグロビンが運搬した酸素を筋肉に溜めることができる。
(3)エ 44.1%

*教科書や資料集に載っていると思う。
コップの底に置いてある見えないコインがある。
コップに水をいれると、コインから出た光が屈折して目に届いて見えるようになる。
水中から空気中へ光が進む場合、水面(境界面)に近づくように曲がる。
光が急に曲がることで目のある方向に光が進む。
@スネルの法則@
光は波の性質をもち、波は異なる物質に入ると屈折で進路を変える。このとき、波はどの程度曲がるのか。
実は入射角と屈折角の関係には一定の法則があり、入射角と屈折角の大きさの比は波の速さの比と等しくなる。屈折後(境界面通過後)の波の速度が大きくなると屈折角も大きくなり、速度が小さくなると屈折角も小さくなる。これをスネルの法則という。(*厳密にいうと角の大きさは高校数学で習う三角比のsinで記述する。公式は難しいのでここでは省略する)
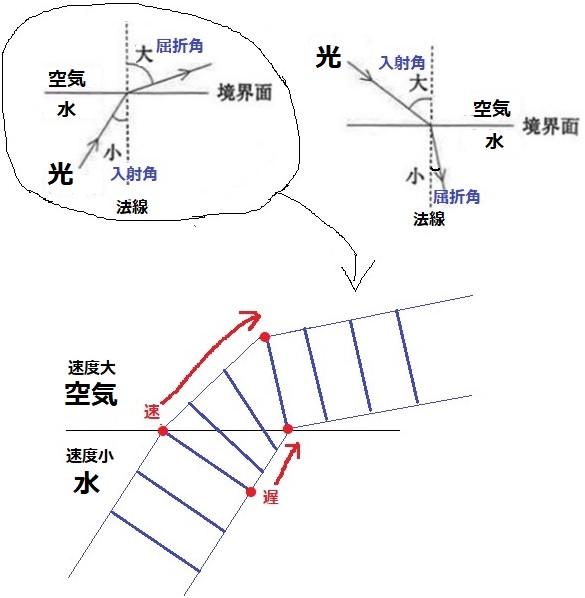
光の速さは水中では遅く、空気中では速い。水→空気では速度が大きくなるので、速度が増した分、屈折角が大きくなって境界面(水面)に近づいて曲がることになる。
スネルの法則を感覚的につかむために、運動会の台風の目を想像しよう。
通常、光は線で表すが、幅のある帯状でとらえる。最初は長い棒が上図のようにゆっくりと平行移動していた。棒の左端がいち早く速度の大きい空気の世界へ突入すると棒の左側は速くなり、まだ速度の小さい水の世界にある右側は相対的に遅い状況にある。台風の目が三角コーンを曲がるときに外側が速く、内側がゆっくり動くのと同じように、棒は速い左側をアウトコース、遅い右側をインコースにして曲がる。境界面をはさんで波の速度変化が大きくなると、曲がり具合も大きくなる。
(4)ウ 45.8%
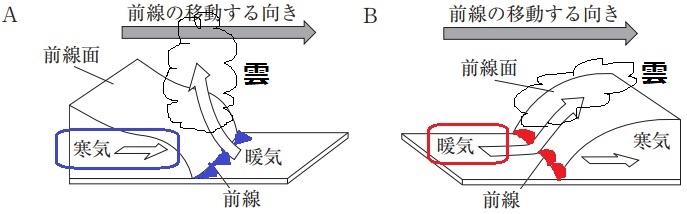
*密度が小さいのは暖気。
空気は暖かくなると密度が小さくなり、風船のように膨らんで浮く。
反対に、冷たくなると密度が大きくなって沈む。
Aは寒気優勢→寒冷前線。Bは暖気優勢→温暖前線。
雲の形に注目しよう!
寒冷前線は寒気が暖気の下を潜り込みながら進む。
縦長の雲(積乱雲)が発生し、狭い範囲に強い雨をもたらす。
温暖前線は暖気が寒気の上を滑り込むように進む。
横に広い雲が発生し、広範囲に弱い雨をもたらす。
(5)エ 52.2%
*計算しないよ!
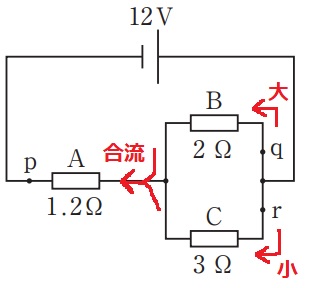
並列は電圧一定。
オームの法則から電圧一定では電流と抵抗は反比例。
抵抗の大きいCは電流が流れにくく、電流量は小さい。
R<Q
合流地点でQ+R=Pになる。
R<Q<P
@余談@
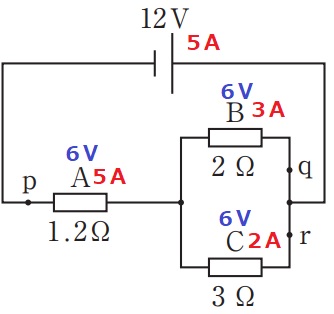
オームの法則で計算するとこうなる。
BとCの合成抵抗は和分の積で(2×3)/(2+3)=1.2Ω
大問2(総合問題)-52.9%
(1)ア 44.0%
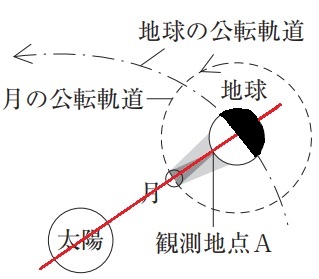
*日食は太陽―月―地球が一直線に並んだときに観察できる。
観測地点Aは太陽に近い12時(正午)
月が太陽の方向にあるので新月である。
月の満ち欠けの周期は約30日で、新月の1週間後は上限の月(右半分)にあたる。
このとき、太陽―地球―月の角度は90°に近くなる。
@@
他方で、月食は太陽―地球―月が一直線に並んだときに観察できる。
太陽と月は正反対の位置にあるので満月。
Super cool view of the Annular Solar Eclipse which passed by our starboard side as we flew over China this morning. A pretty neat way to wake up on Father’s Day morning! Hoping all of the dads in the world have a wonderful day! #Eclipse #FathersDay #HappyFathersDay2020 pic.twitter.com/vJx5yOFAcb
— Chris Cassidy (@Astro_SEAL) June 21, 2020
ISS(国際宇宙ステーション)から撮影された、地球に映る月影だそうです。
(2)イ 39.6%
*フラスコ内に残った水溶液Aは食塩水。
食塩水を蒸発させると食塩の結晶ができる。
単体は1種類の元素、化合物は複数の種類の元素からなる。
食塩(塩化ナトリウム)の化学式はNaCl
ナトリウム(Na)と塩素(Cl)からなる化合物である。
“元素”ではなく、1種類の”物質”は純物質。
複数の純物質が混ざり合うと混合物(食塩水は食塩+水の混合物)
水溶液Aの濃度…水が蒸発で減ったので、食塩水の濃度は高くなる。

JAXAより、水再生システムの仕組み。
水資源の乏しいISSでは人間のおしっこも再利用されている。
(3)エ 72.6%
*動けない植物が生きていくには、葉にどれだけ太陽光をあてられるかが大事になってくる。
植物を上から見ると上下の葉が重なっていないのは、光が当たる面積を増やすため。
師管…栄養分が通る管、道管…水分が通る管
師管は茎の断面では外側、葉の断面では下側にくる。
@フィボナッチ数列と葉序@
1、1、2、3、5、8、13、21、34、55…
前2項の和が連なるフィボナッチ数列は隣り合う2数の比が1:(1+√5)/2(約1.6180339887…)に収束していく。美しい比率とされる黄金比で建築物や企業のロゴなど様々な場面で利用されるが、自然界にも幅広く登場するという。その1つが葉の並び方(葉序)
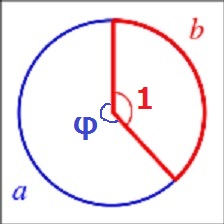
a=(1+√5)/2、b=1
360°をa:bで割ったとき、bの角度を黄金角という。
a=(1+√5)/2=φ(黄金比;ファイ)とすると、
黄金角b=360°×b/(a+b)
=360°×1/(φ+1)=360/φ2=137.5077…°
【*前提知識として、(1+√5)/2はx2-x-1=0のxの解の1つである。
xをφに入れ替えるとφ2-φ-1=0となり、移項してφ2=φ+1が成り立つ】
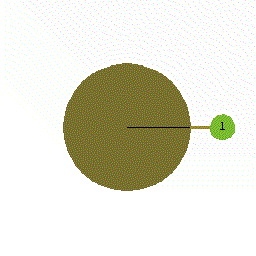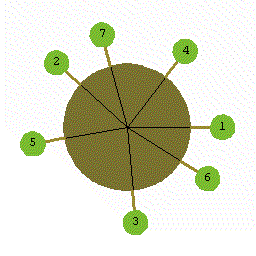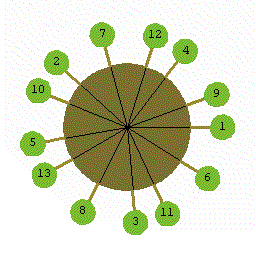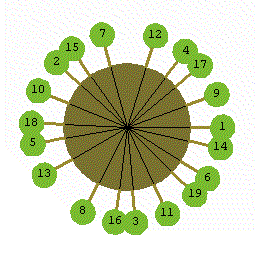
黄金比のいろいろより、幹の周りに黄金角で生える枝葉。
1番目から反時計回りに黄金角(137.5077…)で●を印していくと、
周期性を回避しながら、うまい具合に散らばっている!
進化の過程で植物たちはこの角度に気づいたんですかね(;`ω´)
(4)ウ 55.4%
*『重力が変化しても物体そのものの量(質量)は変わらない』
『月面で同じ質量の物体に働く重力の大きさは地球上の約6分の1になる』
物体Aの質量は地球上でも月面でも300gは変わらない。
一方で、重さは重力の大きさを表すので、重力が変われば重さは変わる。
物体Aを月面ではかりに載せると、重力が6分の1=重さが6分の1になるから約50gを指す。
上皿てんびんの場合、載せた分銅の『重さ』も質量÷6になる。
質量300g同士(重さ50g同士)で釣り合う。
@ニュートン@
力の大きさの単位であるN(ニュートン)
中学理科では100gの物体にはたらく重力の大きさを1Nで表すが、厳密にいうと、「1Nは1kgの質量をもつ物体に1m/s2(メートル毎秒毎秒)の加速度を生じさせる力」と定義される。1kgの物体が1秒間に秒速1mずつ速くなるほどの大きさをもつ力を示す。
地球の重力加速度は約9.8m/s2なので、100g(0.1kg)≒0.98N
重力は地球が地球上の物体を引く力で、重力を計測する場所によってその大きさは異なる。
【重力=地球の引力-遠心力】
低緯度ほど地球の自転による遠心力が強く働くため、重力は小さくなる。

アイザック・ニュートンは万有引力の法則を発見したイギリスの物理学者。万有引力の法則とは、質量をもつすべての物体は引力をもち、2つの物体は互いの引力で引き合うという自然法則。体重60kgの人も60kgに相当する引力を持つことになるが、公式に当てはめて計算すると非常に小さい力ゆえ体感はできない。なぜ、質量をもつ物体は引力をもつのか?アインシュタインの相対性理論によると物体の質量から空間が歪み、周りを引き込む力が生まれるそうです。
@@
重力のない宇宙空間ではどのように重さを計測するのか?
NASAの動画によると、MMDという白い機械のなかに物体を入れて上下に動かしています。
どうやらバネの弾性力で物体に力を加え、その加速度を計測するようです。
質量が小さいと加速度は大きく、質量が大きいと加速度は小さくなります。
●運動方程式;F=ma
F…加える力(Force)、m…質量(mass)、a…加速度(acceleration)
Fが一定の場合、mとaは反比例になる。
大問3(地層)-48.9%
(1)ウ 42.9%
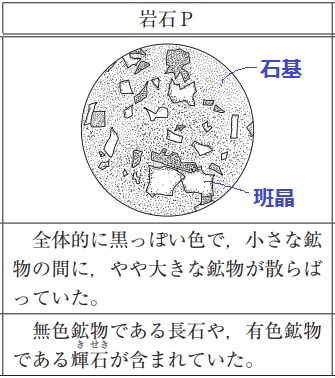
*岩石Pは大きな結晶がまだらに点在している。
マグマが冷えでできる火成岩のうち、火山岩の斑状組織である。
全体的に黒っぽく、輝石がみられることから玄武岩か。
後半が間違いやすい。
礫は角ばっているイメージがあるが、
堆積岩の一種である礫岩の地層は水中で堆積してできた。
河口までたどり着いた礫が海中で積もったので丸みを帯びている。
(2)イ 63.1%
*地層が堆積した地質時代の推定に役立つ化石を示準化石という。
(地層が堆積した当時の環境を推定する化石は示相化石)
フズリナは古生代。魚類と両生類が出現した。
爬虫類も古生代に出現し、中生代に栄える。
哺乳類と鳥類の出現は中生代といわれている。
三葉虫⇒古生代、アンモナイト⇒中生代。
(3)エ 51.8%
*礫・砂・泥の違いは粒の大きさの違いによる。
粒の大きい礫から先に沈む。礫岩の層⇒河口から近い浅い海であった可能性。
粒の小さい泥は遠くに飛ばされて最後に沈む。泥岩の層⇒河口から遠い深い海であった可能性。
やけに耳に残るBGMですが、琉球大学の動画なので内容はちゃんとしてます。
ペットボトルにグラウンドの砂と水を入れてシャッフル。
そのまま放置していると粒子の大きい砂が下に積もる。
粒子の大きいものから順に堆積する構造を級化層理という。
(4)ア 37.8%
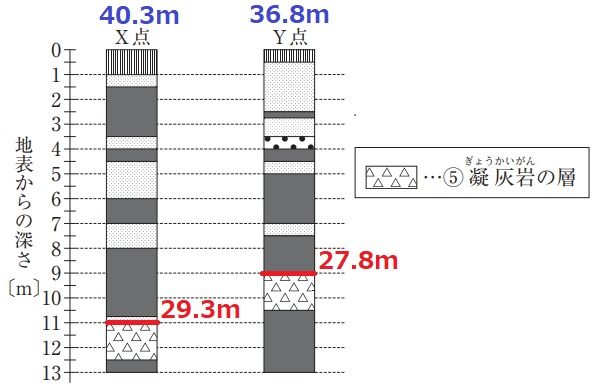
*柱状図に標高を記入しよう。
凝灰岩の層の上部で計算してみる。
X:40.3-11=29.3m
Y:36.8-9=28.7m
図ではX地点の方が低そうだが、実際はXの方がYより1.5m高い。
@かぎ層@
火山灰が堆積した凝灰岩の層は特徴があるゆえ、
離れた地層の新旧を判断する地層の対比によく用いられる。
このような地層を「かぎ層」という。
大問4(遺伝)-59.8%
(1)ウ 71.0%
*エンドウは種子植物―被子植物―双子葉類―離弁花。
双子葉類だから子葉は2枚。子葉が1枚だと単子葉類。
子葉は最初に出てくる葉で、無胚乳種子のエンドウは発芽に必要な栄養分を子葉に貯蔵する。
エンドウは胚珠が子房の中にある被子植物(被る=かぶる)
子房がなく、胚珠がむき出しになると裸子植物で、マツやスギ、イチョウなどがある。
(2)エ 55.4%
*おしべの「やく」から出た花粉がめしべの柱頭について受粉する。
その後、花粉から出た精細胞が花粉管を通って胚珠内の卵細胞と受精する。
動物の場合は精子の核と卵の核が受精して、1つの細胞である受精卵ができる。
精細胞や卵細胞といった生殖細胞は減数分裂で染色体の数が半分しかない。
受精で合体してもとの数に戻る。受精卵に含まれる染色体は7×2=14本
有性生殖はオスとメスの遺伝子の交換から多様な個体が生まれる。
(3)ア 44.0%

*数学の証明問題みたいにカッコが多すぎて読みづらい(;`ω´)
高い遺伝子=A、低い遺伝子=aとする。
結果2(1)よりPは純系AA、結果2(2)よりQは純系aa

PとQを交配させたRの遺伝子はすべてAa
Rは草たけの高い個体だからAが顕性である。
設問はRとQを交配させた結果を問う。
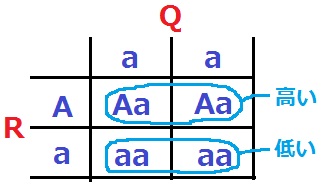
高い:低い=1:1
(4)ウ 68.6%
*情報を整理する。

親は丸、子は丸だけ、孫は丸としわ。
しわが出てくるので潜性遺伝子aは必要→AA×AAはない。
Aa×Aaでは子でaa(しわ)が出てきてしまう。
AA×Aaだと子はすべて丸。Aaを自家受粉させれば孫でaaが出る。
大問5(イオン)-47.3%
(1)イ 67.3%
*高校から降ってきたダニエル電池。
イオン化傾向(イオンへのなりやすさ)が大きい亜鉛が先にイオン化(電離)する。
亜鉛(Zn)が2個の電子を放出して亜鉛イオン(Zn2+)になる。
(負極)Zn→Zn2++2e-(eは電子)
亜鉛イオンは溶液へ。電子は導線を通り、電流が生まれる。
銅板側では硫酸銅水溶液が以下のように電離している。
CuSO4(硫酸銅)→Cu2+(銅イオン)+SO42-(硫酸イオン)
銅イオンが銅板から2個の電子を受け取って、銅板に銅Cuが析出する。
(正極)Cu2++2e-→Cu
(2)ア 41.3%
*負極では亜鉛の電離で溶液中の亜鉛イオンZn2+が増加する。
正極では溶液中の銅イオンCu2+が銅に変わることで減少する。
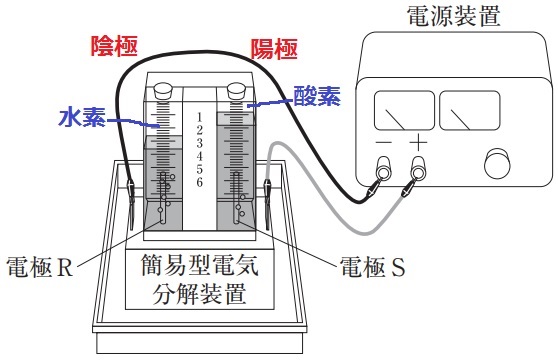
後半は水の電気分解。
-につながる電極Rは陰極、+につながる電極Sが陽極。
2H2O→2H2+O2
陰極に水素H2、陽極に酸素O2が集まる。
体積比は水素:酸素=2:1
図をよくみると陽極の目盛りは1.8に対し、陰極の目盛りは3.6を指している。
Rに集まる水素は空気よりも軽く、Sに集まる酸素は水に溶けにくい。
@余談@
電池では〔正極、負極〕に対し、電気分解では〔陽極、陰極〕と電極の名前が使い分けられている。
ちなみに、水の電気分解で水酸化ナトリウムを混ぜるのは電気を通しやすくするため。
@セロハンの役割@
ダニエル電池のセロハンは溶液を混ぜずにイオンだけを通過させる。
もしセロハンがないと、銅イオンは銅板ではなく直接、亜鉛板から電子を受け取るようになる。
その結果、導線に電子は流れず、亜鉛板に銅が付着する。
また、負極では陽イオン(亜鉛イオン)が増加、正極では陰イオン(硫酸イオン)が増加して
電荷の偏りが生じると、同種のイオンが渋滞して電子の授受がスムーズに行われなくなってしまう。
硫酸イオンがセロハンの穴を通り、負極の亜鉛板側に移動することで、
電気的なバランスが保たれる→電池が安定して機能する。
(3)HCl+NaOH→NaCl+H2O 39.6%
*中和反応の化学反応式。
酸とアルカリを混ぜると、互いに打ち消しあって水H2Oができる。
これを中和反応といい、水と一緒に生成された物質を塩(えん)という。
塩酸…HCl、水酸化ナトリウム…NaOH、塩化ナトリウム…NaCl、水…H2O
まずは指定された順番通りに各物質の化学式を並べる。
HCl+NaOH→NaCl+H2O
質量保存の法則から化学反応の前後で質量は変わらず、各原子の総数は等しくなる。
反応前は水素Hが2個、塩素Clが1個、ナトリウムNaが1個、酸素Oが1個。
反応後も数が等しいから係数はいらない。
(4)ウ 40.9%
*電離式からイオンの増減をみていく。
HCl→H+(水素イオン)+Cl-(塩化物イオン)
NaOH→Na+(ナトリウムイオン)+OH-(水酸化物イオン)
それぞれのイオンは1:1で電離している。
塩酸に水酸化ナトリウム水溶液を入れると、H++OH-→H2Oと中和反応する。
はじめにあった水素イオンH+は中和反応した分だけ減少する。
加えた水酸化物イオンOH-は水素イオンと打ち消しあって0個のまま。
最初からある塩化物イオンCl-は変わらず、ナトリウムイオンNa+は加えた分だけ増加。
【H+減、OH-無し、Cl-不変、Na+増】
1:1の電離からH+の減少分とNa+の増加分が相殺されてイオンの総量は変わっていない。
BTB溶液が緑になった中性の状態でH+とOH-がなくなる。
H+がないと中和反応が起こらないので、以降はNa+とOH–が増加する→イオンの総数も増加。
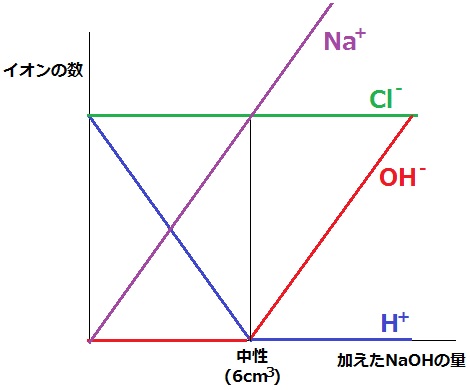
グラフを描くとこのような感じになる。
中性まではイオン全体の総数は変わず、中性後に増加する。
大問6(運動)-59.1%
(1)ア 68.1%
*レールAの⑧~⑩をみる。
時間は0.3秒間
移動距離は、10.6+9.0+5.6=25.2cm
速さは、25.2÷0.3=84cm/s=0.84m/s
(2)イ 46.8%

*先に速さの変化から確認する。
レールBの①~③において、0.1秒毎の移動距離の差をとると2.4cmで等しい。
速度の変化率(加速度)が等しい等加速度直線運動である(イかエ)
また、小球が等加速度直線運動をしたということは、Bの①~③は直線のレールである。
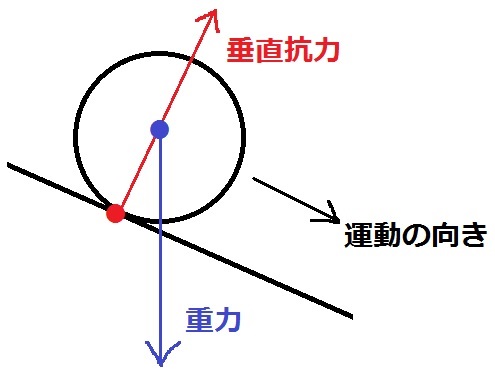
まず、斜面を運動する小球には2つの力が働いている。
1つは重力。もう1つは斜面から受ける垂直抗力(中学の範囲なので摩擦は考えない)
このうち、『小球が運動する向きに働く力』を考える。

斜面上にある物体に働く重力は分解される。
斜面に垂直な分力は垂直抗力とつり合っているので無視する。
残りの斜面に平行な分力が小球を転がす力、すなわち「小球が運動する向きに働く力」にあたる。
重力は変わらない、かつレールが直線ゆえ重力の分解の仕方も変わらないことから、
斜面に平行な分力の大きさ(上図の赤い矢印の長さ)は一定である。(イ)
(3) 64.9%

*力の分解を作図する。力の内容は先に書いた通り。
重力を対角線とする長方形をつくり、2つの矢印を描く。
レールB⑨は小球が斜面を登っていく。
斜面に平行な分力が小球が運動する向きの反対側になり、小球はしだいに遅くなっていく。
(4)イ 56.4%
*力学的エネルギー保存の法則…運動エネルギーと位置エネルギーの和が一定。
ボールのスタート地点はレールAもBも高さは9cm。
bはeより低いので、eより位置エネルギーが小さく、運動エネルギーが大きい。
cとfは高さ0cmだから、運動エネルギーはほぼ等しい。
@最速降下曲線@
奥から順に①直線、②円弧、③サイクロイド曲線、④楕円の一部。
球が一番早くゴールにたどり着く坂はどれでしょうか?
・・妙な名前の③です。
動画の後半にはサイクロイド曲線の説明があります。最後に出てくる等時性とは、
サイクロイド曲線のどこから球を転がしても最下点に着く時間が同じになることをいいます。
秋山仁先生は有名な数学者のお一人です。



コメント