2023年度　千葉県公立高校入試問題過去問【数学】解説

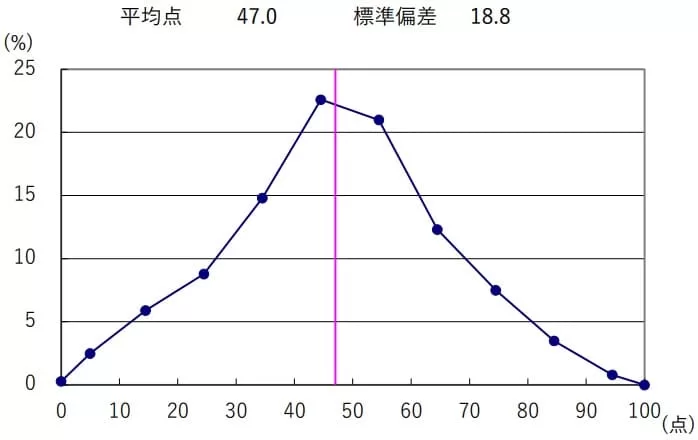
平均47.0点（前年比；－4.5点）

問題はコチラ→ＰＤＦファイル

大問１（小問集合）―59.6％

（１）①　94.7％
６÷（－２）－４
＝－３－４
＝－７

②　77.8％
ａ＋ｂ＋１/４（ａ－８ｂ）
＝ａ＋ｂ＋１/４ａ－２ｂ
＝５/４ａ－ｂ

③　72.1％
（ｘ－２）²＋３（ｘ－１）
＝ｘ²－４ｘ＋４＋３ｘ－３
＝ｘ²－ｘ＋１

（２）①　65.8％
５ｘ²－５ｙ²
＝５（ｘ²－ｙ²）
＝５（ｘ＋ｙ）（ｘ－ｙ）

②　53.6％
前の式にｘ＝√３＋２、ｙ＝√３－２を代入。
５（ｘ＋ｙ）（ｘ－ｙ）
＝５｛（√３＋２）＋（√３－２）｝｛（√３＋２）－（√３－２）｝
＝５×２√３×４
＝40√３

（３）①　68.2％
40÷240
＝１÷６＝0.166…≒0.17

②　78.4％
ア：範囲（レンジ）＝最大値－最小値
　箱ひげ図から、125－30＝95回×
イ：70回以上90回未満の階級の累積度数→小さい順に足す。59＋79＋37＝175人×
　102人は大きい順に25＋40＋37と足している。
ウ：度数が最も少ない階級→110～130回の階級。階級値は110と130の平均で120回。〇
エ：箱ひげ図から第３四分位数は95回。×
　第１四分位数は50回である。
ウ

（４）①　66.7％

立方体の各面の中心を結ぶと正八面体になる。
ＢＤとＣＥの交点Ｏは立方体の中心。
正面から見ると四角形ＡＢＦＤは正方形で、△ＡＢＤは直角二等辺三角形。
辺の比は１：１：√２だから、ＢＤ＝√２ｃｍ

②　29.7％！

ＢＤ＝√２ｃｍは立方体の１辺に相当する。
ＣＥもＡＦも√２ｃｍである。
正八面体を四角錘Ａ―ＢＣＤＥと四角錘Ｆ―ＢＣＤＥに分け、
この２つの合同な四角錘の高さの和がＡＦ＝√２ｃｍに相当する。
正八面体の体積は、√２×√２÷２×√２÷３＝√２/３ｃｍ³

（５）①　46.9％
【３、６、９】から２枚を選ぶ。
₃Ｃ₂＝３通り

②　52.7％
６枚から２枚選ぶ組み合わせは、₆Ｃ₂＝15通り
余事象で攻める。積が３の倍数にならない→【１・４・８】から２枚選ぶ。
₃Ｃ₂＝３通り
積が３の倍数になる→15－３＝12通り
確率は、12/15＝４/５

（６）①　87.4％
ｙ＝１/３ｘ²にｘ＝－３を代入。
ｙ＝１/３×３²＝３

②　22.8％！

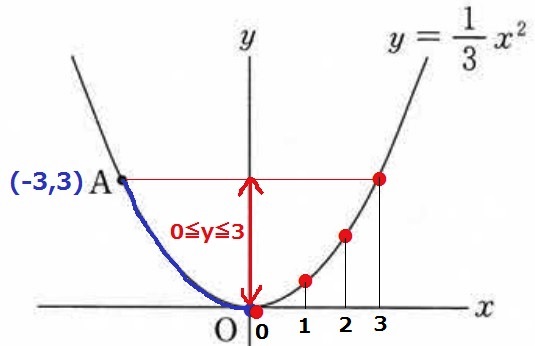
０≦ｙ≦３となる整数ａを考える。
ａ＝０のときに最小値ｙ＝０を確保できる。
ａ＝３まで条件を満たす。
ａ＝０、１、２、３

（７）６点―17.0％！、３点―6.5％、無答―27.2％
円が内接する三角形を作図する。

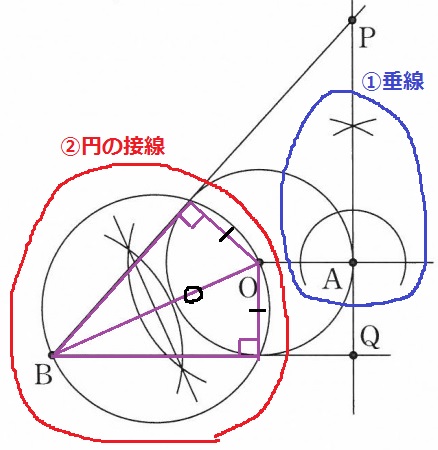
①『点Ａを接点とする円Ｏの接線』→ＯＡをひき、Ａを通る垂線を描く。
②『点Ｂから円Ｏにひいた２本の接線』→ＯＢの垂直二等分線、中心から円を作図する。
（直径ＢＯに対する円周角は90°、共通辺ＢＯと円の半径から２つの直角三角形は合同）
接線と半径は直交する。
Ｂから２つの円の交点に向かって直線をひき、①との交点がＰとＱ。
ＡＰ＞ＡＱより、上がＰ、下がＱとなる。

大問２（関数）―40.4％

（１）①　89.0％
ｙ＝４ｘにｙ＝８を代入。
４ｘ＝８
ｘ＝２

②　27.9％！

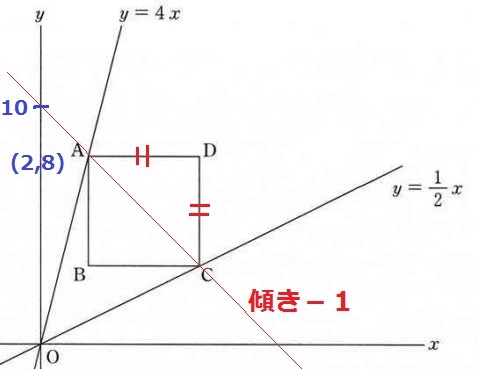
Ｃ座標は不明だが、ＡＤ＝ＤＣ。
△ＡＣＤは直角二等辺三角形で斜辺ＡＣの傾きは－１。
Ａから左に２、上に２移動して、切片は８＋２＝10
ｙ＝－ｘ＋10

（２）　4.4％!!

直線上にあるＡとＣの座標がポイントになる。
Ａのｘ座標をｔとすると、Ａ（ｔ、４ｔ）
ＡとＣのｘ座標の平均が13だから、その和は26である。
Ｃのｘ座標は26－ｔ。これをｙ＝１/２ｘに代入して、Ｃ（26－ｔ、13－ｔ/２）

赤線の直角二等辺の等辺で等式を立てる。
５ｔ＝39－３/２ｔ
ｔ＝６

Ｄのｘ座標は、26－ｔ＝26－６＝20
ｙ座標は、４ｔ＝４×６＝24
Ｄ（20、24）

＠別解＠
( ﾟAﾟ)ﾔﾍﾞｰ

２つの直線に挟まれた正方形が右上に平行移動すると相似に拡大する。
ＡＣは対角線。Ａ座標が決まると対角線の式からＣ座標が決まる。
ＡとＣが決まるとＢとＤの座標も決まり、正方形の位置が確定する。
正方形の中心も同様に位置が定まり（ACの中点）、その軌跡を結ぶと原点を通る直線である。

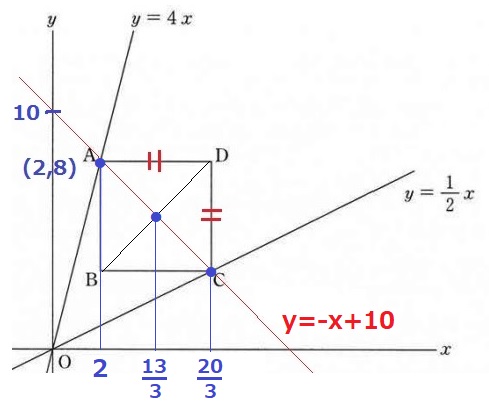
（１）の正方形の中心を調べてみる。
Ｃはｙ＝１/２ｘとｙ＝－ｘ＋10の交点だからＣのｘ座標は、
１/２ｘ＝－ｘ＋10
ｘ＝20/３
ＡとＣのｘ座標を平均すると、中心のｘ座標は（２＋20/３）÷２＝13/３ (´･_･)ﾝ？

（１）と（２）を融合させると上図のようになる。
中心点のｘ座標13/３を３倍すると、ちょうど13なので、
（１）の各頂点座標を３倍すると（２）の頂点座標になる。
Ｃのｘ座標…20/３×３＝20
Ａのｙ座標…８×３＝24
よって、Ｄ（20、24）
ﾆｸｲﾈｪ(・ㅂ・)

大問３（平面図形）―29.9％

（１）　80.9％

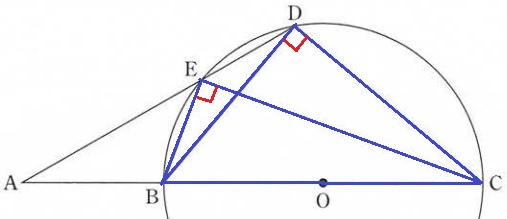
直径に対する円周角を探す。
∠ＢＥＣ＝∠ＢＤＣ＝90°
ａ…イ、ｂ…エ、ｃ…90°

（２）６点―8.7％!!、３点―4.0％、無答―33.8％
△ＡＢＥ∽△ＡＤＣの証明。

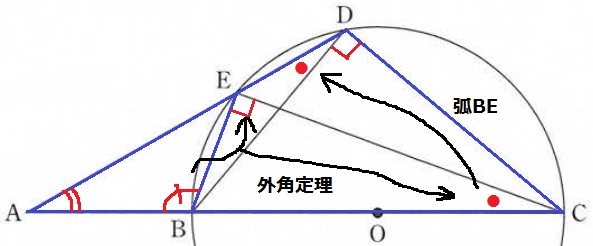
共通角で∠ＢＡＥ＝∠ＤＡＣ
∠ＡＢＥを外角定理で90°＋●に分解。
前問の90°を利用、弧ＢＥに対する円周角で●を移動すると、∠ＡＢＥ＝∠ＡＤＣ
２角が等しく∽。

＠別解＠

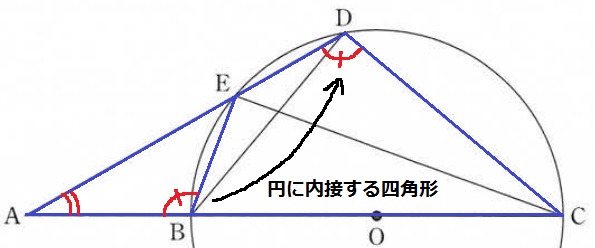
『外角はそれと隣り合う内角の対角に等しい』という円に内接する四角形の性質を知っていれば、
四角ＢＣＤＥが円に内接するので、∠ＡＢＥ＝∠ＡＤＣを指摘できる。

（３）　０％!!!?

おそらく大方の生徒はここまでいけたはず。
△ＡＦＥの内角から辺の比は１：２：√３→ＡＥ＝３√３ｃｍ、ＡＦ＝６ｃｍ
…が、ここから筆が進まない(°ㅂ°҂)

ＡＢは外側にあって手出しが難しい。ＢＦが知りたい。
１：２：√３が頭を支配し、辺の情報が左側に偏ってあくどい構図だが、
ＢＦを１辺とする相似図形が見つかるのを祈る。

Ｅには90°が密集している。
∠ＡＥＢ＝●、∠ＢＥＦ＝×として、●＋×＝90°の角度調査をすると上図のようになる。

弧ＤＣの円周角より、∠ＧＢＦ＝×
２角相等で△ＧＢＦ∽△ＢＥＦ。
ＢＦ：ＧＦ＝ＥＦ：ＢＦ
ｘ：２＝３：ｘ
外項と内項の積から、ｘ²＝６
ｘ＞０より、ｘ＝√６
したがって、ＡＢ＝ＡＦ－ＢＦ＝６－√６ｃｍ
*３√３は不要でした(^ω^)????

大問４（方程式）―37.3％

（１）①ａ　83.8％
Ａはグー負け、チョキ勝ち、グー勝ち。
－１＋２＋１＝２点

ｂ　49.2％
グー勝ち…１点、チョキ勝ち…２点、パー勝ち…５点
書き出しが無難だと思う。
（グ、グ）＝２点
（グ、チョ）＝３点
（グ、パ）＝６点
（チョ、チョ）＝４点
（チョ、パ）＝７点
（パ、パ）＝10点
以上、６通り。

ｃ　53.6％
Ａが２回目勝ちで９点を超えるのは、（パ、パ）の10点だけ。
３回目にグーで負ければ－１点で９点になる。
Ｂはグー負け・グー負け・パー勝ちになる。
－１－１＋５＝３点

②ｄ　27.1％！
どちらかがグー勝ち…ａ回、チョキ勝ち…ｂ回、パー勝ち…ｃ回
じゃんけんは合計10回だから、ａ＋ｂ＋ｃ＝10
ｃ＝10－ａ－ｂ

ｅ　8.6％!!
【グー】－１点がａ回。
【チョキ】－３点がｂ回。
【パー】４点が10－ａ－ｂ回。
Ｍ＝－ａ－３ｂ＋４（10－ａ－ｂ）
＝－ａ－３ｂ＋40－４ａ－４ｂ
＝－５ａ－７ｂ＋40

（２）４点―1.5％!!、２点―1.2％、無答―82.8％!!
不定方程式。

公式解答より。
２人の持ち点の合計が０点→Ｍ＝０
前問の式を活用する。
－５ａ－７ｂ＋40＝０
ａについて解くと、ａ＝８－７/５ｂ
ａは０以上10以下の整数→８が整数だから、７/５ｂも整数でなくてはならない。
ｂ＝０、５
それぞれを代入すると、（ａ、ｂ、ｃ）＝（１、５、４）（８、０、２）

■追記■

正答率0.0％は他県で何度か見かけたことあるが、０％は初なので刻んでおきます。
注釈、役に立ちましたね(´・_・`)
不定方程式も正答率が悪かった。経験してなかったか、それとも時間不足なのか。
今年度は不定方程式の設問をいくつかを見かけたので、出題されなかったところは来年要注意！

＠2023年度・千葉解説＠
社会…平均54.5点　理科…平均60.7点　英語…平均47.6点　国語…平均47.9点
思考力を問う問題…数英国の３教科。来年度は千葉・千葉東・東葛飾が対象。
公立高校入試解説ページに戻る