2019年度　山形県公立高校過去問【数学】解説

問題はコチラ→ＰＤＦファイル

大問１（小問集合１）

（１）①　96.2％
－３－（－8）＋１
＝－３＋８＋１
＝６

②　87.2％
－１/４＋４/９÷２/３
＝５/12

③　77.4％
（24ｘ²ｙ－15ｘｙ）÷（－３ｘｙ）
＝－８ｘ＋５

④　75.3％
（√６－２）²＋√54
＝６－４√６＋４＋３√６
＝10－√６

（２）　83.0％
ｘ²－６ｘｙ＋９ｙ²
＝（ｘ－３ｙ）²　←ここで代入
＝（９/２－３×１/２）²
＝３²＝９

（３）　86.8％
（ｘ＋４）（ｘ－３）＝７ｘ－８
ｘ²＋ｘ－12＝７ｘ－８
ｘ²－６ｘ－４＝０
因数分解ができないので解の公式を適用する。
ｂ＝２ｂ’ver.が使える。
ｘ＝３±√13

（４）　69.4％
全体の取り出し方…６×５＝30通り

異なる色の出し方…
（赤→白）４×２＝８通り
（白→赤）同じく８通り、
よって、16/30＝８/15

（５）　52.4％
ＨＭ＝６÷２＝３ｃｍ
△ＯＨＭで三平方。
ＯＭ＝√（９²－３²）＝６√２ｃｍ

大問２（小問集合２）

（１）①　81.9％
原点を通ることに注意！
ｘ＝０のとき、最小値ｙ＝０
ｘ＝４のとき、最大値ｙ＝８
０≦ｙ≦８

②　49.0％
ｙ＝１/２ｘ²に代入。
Ａ（－２、２）Ｂ（４、８）
Ａの座標から反比例の式を求める。
２＝ａ/－２
ａ＝－４⇒ｙ＝－４/ｘ
Ｃ（４、－１）

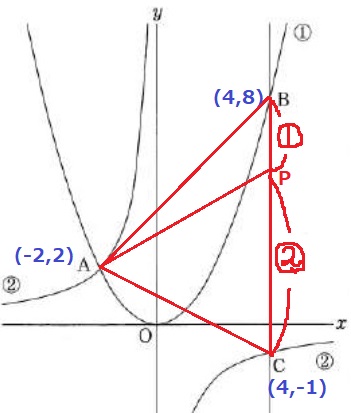
△ＡＣＰと△ＡＢＰの面積比が２：１
⇒ＢＰ：ＰＣ＝１：２なので、
Ｐのｙ座標は、－１＋９×２/３＝５
ウ

（２）①　78.5％
求める値は４月の博物館の入館者だが、
３月の入館者を基準に増減の％が与えられているので、３月の博物館の入館者をｘ人とする。
３月の美術館の入館者を7200－ｘ人とおくと１次方程式、ｙとおくと連立方程式になる。

１次方程式だと、
0.1ｘ－0.02（7200－ｘ）＝312

連立方程式だと、
ｘ＋ｙ＝7200
0.1ｘ－0.02ｙ＝312

②　31.9％！
以上の式を解くと、ｘ＝3800
３月の博物館の入館者が3800人。
４月の博物館の入館者はこれの１割増しなので、
3800×11/10＝4180人

（３）　53.5％（50～99％：8.3％、１～49％：5.2％）
説明問題。各々の相対度数を比べてお終い。
240ｃｍ以上260ｃｍ未満の階級において、
Ａ中学校の相対度数は９÷75＝0.12
Ｂ中学校の相対度数は７÷50＝0.14
Ｂ中学校の方が相対度数が大きい。

（４）　72.2％
作図問題。レベルは易しい。
①ＡＤの長さと等しい⇒Ａを中心、ＡＤを半径とした円を描く。
②ＡＢとＢＣから等しい距離にある⇒∠ＡＢＣの二等分線
交点は２つできる。『△ＡＢＣの外部の点』がＰとなる。

大問３（数量変化）

（１）①　73.6％
ｙ＝14までは給水スピードが毎秒200ｃｍ³で一定なので、
（ｘ、ｙ）＝（８、10）の関係がｘ＝４のときにも当てはまる。
ｘ＝４のときのｙの値は、ｙ＝10×４/８＝５

②　ア：38.9％　イ：51.7％　ウ：29.5％！　グラフ：68.8％
０≦ｘ≦８は前問と同様。
ｘ＝４のときｙ＝５なので、ｙ＝５/４ｘ

つぎの転換点は、給水速度が変わるｙ＝14（水面の高さが14ｃｍ）のとき。
８≦ｘ≦14ではｙ＝１/２ｘ＋６と式が与えられているので、これにｙ＝14を代入する。
14＝１/２ｘ＋６
ｘ＝16

16≦ｘ≦22のとき、給水速度が２倍になるので傾きも２倍になる。
先ほど、傾きが１/２だったので傾きは１。
ｘ＝16のとき、ｙ＝14なので、これらをｙ＝ａｘ＋ｂに代入。
14＝16×１＋ｂ
ｂ＝－２
よって、ｙ＝ｘ－２
ア：16　イ：５/４ｘ　ウ：ｘ－２

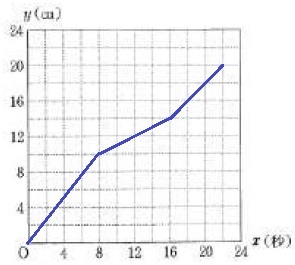
傾きが変わるところは、底面積が変わる（８、10）、給水速度が変化する（16、14）。
傾きが２倍となり、（22、20）でフィニッシュ。

（２）　6.9％!!
体積比は正面からの面積比でとらえる。

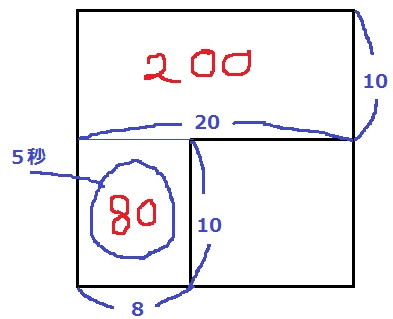
奥行きはどこも20ｃｍなので、面積比が体積比となる。
左下の80ｃｍ²のところを満たすのに５秒かかった。
全体では、５×280/80＝35/２秒後

大問４（平面図形）

（１）　68.8％

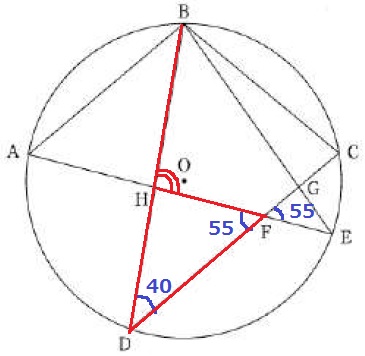
対頂角で55°を移す。
△ＨＦＤで外角定理→∠ＢＨＥ＝55＋44＝95°

（２）　11.8％！（50～99％：15.6％　１～49％：24.7％）
△ＡＨＢ∽△ＦＧＥの証明。

ＡＢ//ＤＣより、同位角（×）が等しい。
同じく、錯角でおろし、孤ＡＢ＝孤ＢＣから円周角（●）が等しい。
２角が等しく、∽。

（３）　2.8％!!
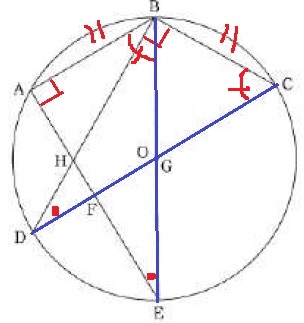
半径しか長さが与えられていない状態で、変な四角形を求めさせられる。
長さの情報が不足しているときは、角度を調べよう。
角度→特別な図形→新しい辺の長さがわかる。

△ＡＢＥと△ＢＣＤに注目。

直径で長さが等しい（ＢＥ＝ＣＤ）。
直径に対する円周角は直角（∠ＢＡＥ＝∠ＣＢＤ）。
等しい弧に対する円周角は等しい（∠ＡＥＢ＝∠ＢＤＣ）。
残りも角も等しくなる（∠ＡＢＥ＝∠ＢＣＤ）
→一辺両端角相等で△ＡＢＥ≡△ＢＣＤ

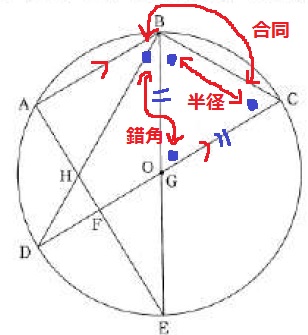
次は△ＢＣＧに注目する。
半径より、△ＢＣＧは二等辺（∠ＧＢＣ＝∠ＧＣＢ）
合同から、∠ＧＣＢ＝∠ＡＢＧ
ＡＢ//ＤＣから、錯角で∠ＡＢＧ＝∠ＢＧＣ
以上より、△ＢＣＧの内角がすべて等しくなる。
→△ＢＣＧは正三角形

30°ー60°－90°の直角三角形をフル活用。
辺の比は１：２：√３

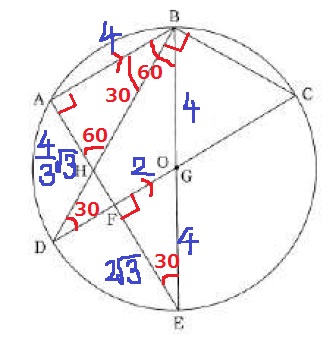
△ＡＢＥにおいて、ＢＥ＝８ｃｍより、
ＡＢ＝４ｃｍ、ＡＥ＝４√３ｃｍ

ＡＢ//ＤＣより、∠ＥＦＧ＝90°
△ＥＦＧで１：２：√３
ＧＦ＝２、ＦＥ＝２√３

錯角より、∠ＨＤＦ＝∠ＨＢＡ＝30°
△ＡＢＨで１：２：√３
ＡＨ＝４√３/３

４×４√３÷２ー４×４√３/３÷２－２√３×２÷２
＝８√３－８√３/３－２√３
＝10√３/３ｃｍ²
公立高校入試解説ページに戻る