問題PDF
図1のような1辺の長さが1cmの立方体ABCDEFGHから「頂点を切り落とす」ことを考えます。たとえば「頂点Bを切り落とす」とは、3点A、C、Fを通る平面で立方体を切断し、点Bを含む方を取り除くことを言います。同じように、「頂点Hを切り落とす」とは、3点D、E、Fを通る平面で立方体を切断し、点Hを含む方を取り除くことを言います。例として、2つの頂点B、Hを同時に切り落としてできる立体は図2のようになります。次の問いに答えなさい。

(1)
立方体ABCDEFGHから2つの頂点B、Hを同時に切り落としてできる立体の体積は何cm3ですか。
(2)
立方体ABCDEFGHから4つの頂点A、B、G、Hを同時に切り落としてできる立体について、
①
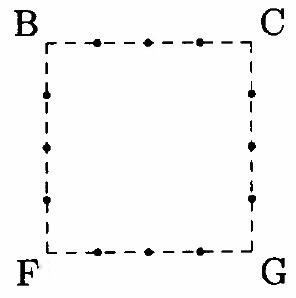
この立体の表面を黒く塗って、面BFGCの方向から見たとき、
黒く塗られている部分を解答らんの図に書き込み、斜線で示しなさい。
ただし、辺上の点は各辺を等分した点です。
②
この立体の体積は何cm3ですか。
(3)
立方体ABCDEFGHから8つの頂点A,B、C、D、E、F、G、Hを
同時に切り落としてできる立体の体積は何cm3ですか。
@解説@
(1)
立方体から2つの三角錐をひく。
1×1×1-1×1÷2×1÷3×2=2/3cm3
(2)①
豊島岡女子のような難易度の高い切断。
初期状態がすでに複雑なのに、さらに2回切断するという…。

わかりやすいAから。
切断面の線は立体の側面をなぞるように図示する。
不要な線を消すと右図のような八面体なる。
ここからGを切り落とすが…アングルがかなり厳しい。。

宝石のカットにありそうな形になる。

これを面BFGCから眺めるとこうなる。(解答欄では斜線で表すこと!)
G側の作図がキツイ。
反対側も対称的に切断するので、A側で起きたことはG側でも起こるはず。
面BFGC上でB側(A側)で直角二等辺角形の空白ができるとわかれば、
G側でもそうなるのでは?と想像して解答欄を埋め込むしかないような…。
②
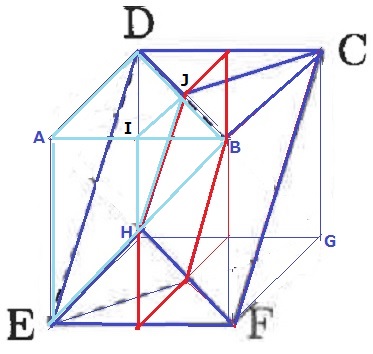
三角錐B-IJHと三角錐B-ADEの体積比は1:8
角錐台IJH-ADEの体積は、1×1÷2×1÷3×7/8=7/48cm3
これと同じ図形があと3つある。
立方体から、4つの合同な角錐台をひく。
1×1×1-7/48×4=5/12cm3
(3)

8つの頂点を切り落とすと、正八面体があらわれる。
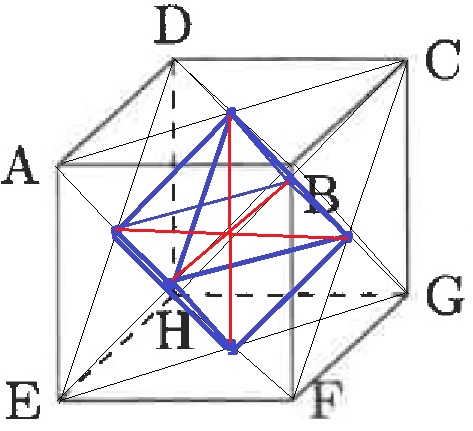
赤い線が1cm。
対角線が1cmである正方形を底面とする、高さの合計が1cmの2つの正四角錐の体積。
1×1÷2×1÷3=1/6cm3



コメント