2020年度　武蔵中学過去問【算数】大問２解説

問題ＰＤＦ
図のように、角Ａと角Ｂが直角の台形ＡＢＣＤがあり、ＡＤ：ＢＣ＝３：８です。
また、三角形ＡＢＥの面積と台形ＡＢＣＤの面積の比は５：11です。
次の各問に答えなさい。

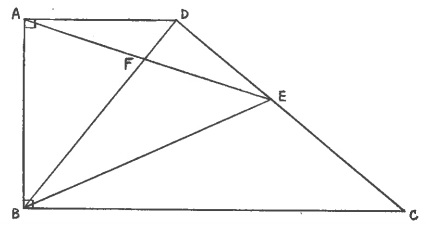
（１）ＤＥ：ＥＣを求めなさい。

（２）ＤＦ：ＦＢを求めなさい。

＠解説＠
（１）
台形ＡＢＣＤの面積比が【11】で上底と下底の比が３：８。
３＋８＝11…
台形の面積比は上底＋下底の和で表せるので、△ＡＢＥを等積変形させて上底にくっつける。

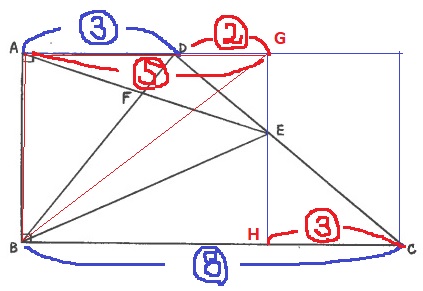
Ｅを通るＡＢに平行な線分をひく。
ＡＤの延長線とＢＣとの交点をそれぞれＧ、Ｈとする。
台形ＡＢＣＤの面積比が【11】で、上底＋下底＝⑪
△ＡＢＥ＝△ＡＢＧの面積比が【５】だから、ＡＧ＝⑤
ＤＧ＝⑤－③＝②

△ＤＥＧと△ＣＥＨの相似から、
ＤＥ：ＥＣ＝ＤＧ：ＣＨ＝２：３

（２）
△ＡＤＥと△ＡＢＥにおいて底辺をＡＥとしたとき、ＤＦ：ＦＢはこれらの高さの比にあたる。
そこで、△ＡＤＥと△ＡＢＥの面積比を求める。

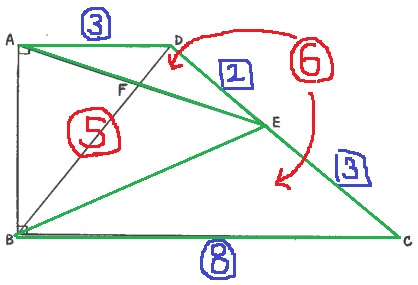
△ＡＢＥの面積を⑤とおくと、△ＡＤＥと△ＢＣＥの面積の和が⑥になる。
この２つの三角形は２辺の比がわかっているので、
隣辺比から△ＡＤＥ：△ＢＣＥ＝３×２：８×３＝１：４
△ＡＤＥ＝⑥×１/５＝〇６/５
ＤＦ：ＦＢ＝〇６/５：⑤＝６：25
難関中（算数科）解説ページに戻る