2024年度　ラ・サール中学過去問【算数】大問６解説

問題ＰＤＦ
３辺の長さが１ｃｍ、１ｃｍ、３ｃｍの直方体６本を
図のように組み上げて１つにした立体があります。

（１）
この立体の表面積は何ｃｍ²ですか。

（２）
この立体を３点Ａ、Ｂ、Ｃを通る平面で切ると、３つの立体に分かれます。
これら３つの立体の体積はそれぞれ何ｃｍ^３ですか。
ただし、角すいの体積は（底面積）×（高さ）÷３です。

＠解説＠
（１）

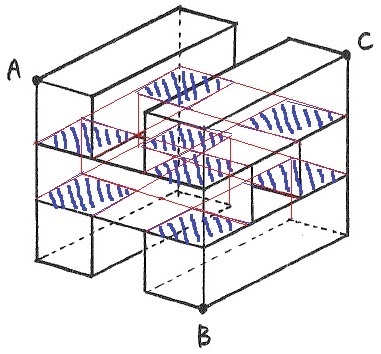
直方体６本の表面積から接している部分を引く。
６本の表面積は、（４×３＋２）×６＝84ｃｍ

（２）

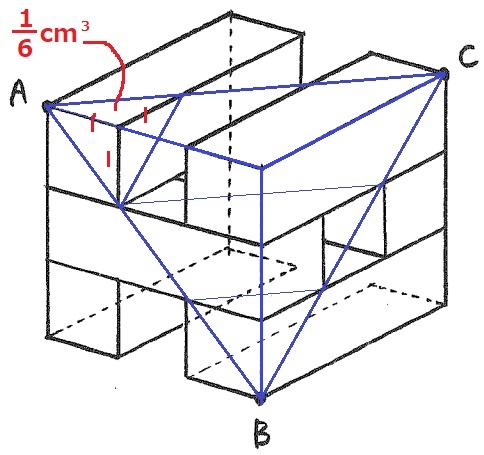
まず、左上の三角錐が分離される。
１×１÷２×１÷３＝１/６ｃｍ³

大きな三角錐は、３×３÷２×３÷３＝９/２ｃｍ³
２つ目も手前側に目をつける。

大きな三角錐から空白の部分を引く。
ＡＢ・ＢＣ・ＣＡに平行な線と、直方体の辺との交点に印をつけて立体を分析する。
右下の空白は１/６ｃｍ³の三角錐。
左上の空白は断頭四角柱で高さを均すと１ｃｍ→１×１×１＝１ｃｍ³
２つ目の立体の体積は、９/２－（１＋１/６×２）＝19/６ｃｍ³
３つ目は、１×１×３×６－（１/６＋19/６）＝44/３ｃｍ³
１/６ｃｍ³、19/６ｃｍ³、44/３ｃｍ³
難関中（算数科）解説ページに戻る