問題PDF
1辺の長さが12cmである立方体の形をした水そうがあります。下の図のように、この水そうを水平な机の上に置き、頂点にそれぞれA~Hの記号を付けます。また、対角線CEを4等分してCに一番近い点をKとします。この水そうにいろいろな量の水を入れて、ふたをします。このとき水面が次の(1)~(3)の状態になるときの水そうに入っている水の体積はそれぞれ何cm3ですか。

(1)
辺EHを机につけたまま、真上から見たときに辺BCと辺EHが重なるように水そうをかたむけたところ、水面がCDの真ん中の点を通った。
(2)
頂点Eを机につけたまま、真上から見たときに頂点Cと頂点Eが重なるように水そうをかたむけたところ、水面が頂点Dを通った。
(3)
頂点Eを机につけたまま、真上から見たときに頂点Cと頂点Eが重なるように水そうをかたむけたところ、水面が点Kを通った。
@解説@
(1)
面AEBF方向からとらえる。
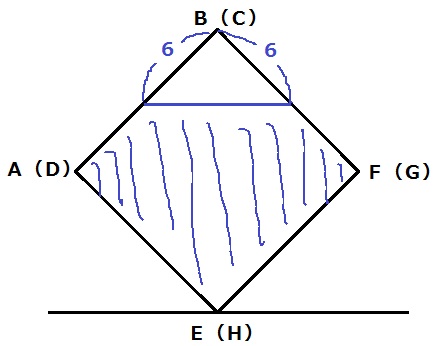
青い斜線の面積は、12×12-6×6÷2=126cm2
奥行きは12cmなので、126×12=1512cm3
(2)
なんとなくこうなるんじゃないかと頭の中で思い浮かべても作図が大変。
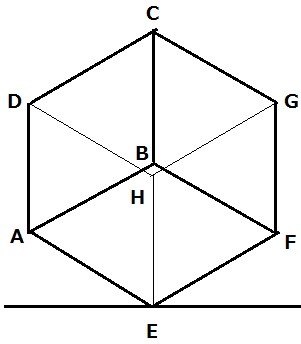
↑こんな感じ。
Dに水面があるということなので、Dを通り、地面に平行な面を作図。

CからB、D、Gまでの距離はそれぞれ等しい。
立方体を問題文のように傾けたとき、水面は面DBGとなる。
12×12×12-12×12÷2×12÷3=1440cm3
(3)
△DBGの各辺は、立方体の側面である正方形の対角線で長さがすべて等しい。
⇒△DBGは正三角形。
CB=CD=CGなので、Kを通る水面も△DBGと相似図形になりそう。
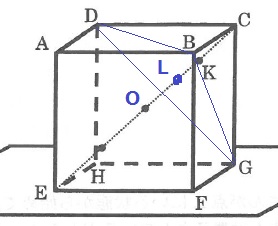
面DBGとCEとの交点をLとする。
対角線CEの中点は立方体の中心で、ここをOとする。
LK:KCの値がわかれば、Kを通る水面の正三角形の1辺がわかりそう。
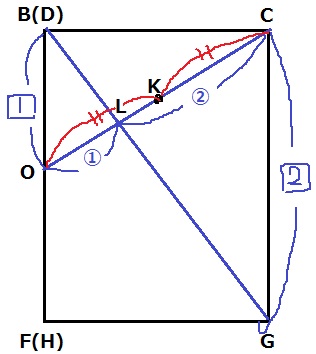
立方体を時計回りに45°傾け、面AEGCの右半分を考える。
△BOL∽△GCLで、BO:GC=OL:CL=1:2
KはOCの中点。
連比を組むと、OL:LK:KC=2:1:3
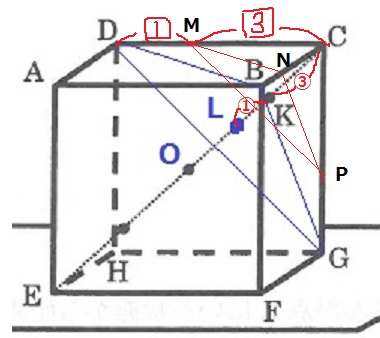
Kを通り、正三角形DBGに平行な面を正三角形MNPとおく。
三角錐C-MNPと三角錐C-DBGは全体で相似。
DM:MC=LK:KC=1:3
MC=12×3/4=9cm
MC=NC=PC=9cm
12×12×12-9×9÷2×9÷3
=1728-121.5=1606.5cm3



コメント