問題ＰＤＦ
１辺が１ｃｍの２種類の立方体Ａ、Ｂがあります。
立方体Ａは重さが５ｇで表面が白く塗られていて、
立方体Ｂは重さが７ｇで表面が黒く塗られています。
次の〔 〕に適当な数を入れなさい。
（１）
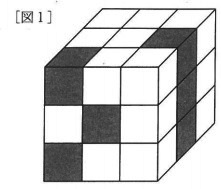
立方体Ａと立方体Ｂを合わせて27個使って、
〔図１〕のような１辺が３ｃｍの立方体を作りました。
この立方体全体の重さは最も軽い場合で〔 ア 〕ｇ、最も重い場合で〔 イ 〕ｇです。
（２）
次に、立方体Ａと立方体Ｂを合わせて64個使って、１辺が４ｃｍの立方体を作ったところ、
その重さは378ｇでした。この立方体の表面全体のうち、黒く塗られている部分の面積の和は、
最も小さい場合で〔 ア 〕ｃｍ2、最も大きい場合で〔 イ 〕ｃｍ2です。
＠解説＠
（１）
黒は見える部分だけにあるとする。
黒は６個で、７×６＝42ｇ
白は27－６＝21個で、５×21＝105ｇ
最も軽い場合は、42＋105＝147ｇ（ア）
図１の状態で見えない立方体は左奥の８個。
１個の白を黒に切り替えると２ｇ増える。
147＋２×８＝163ｇ（イ）
（２）
まずは各々の個数を求める。
白５ｇ、黒７ｇ、計64個で378ｇ。
鶴亀算の材料がそろっているのでツルカメ。
64×７－378＝70
70÷（７－５）＝35
白は35個、黒は29個となる。
続いて、黒29個の配置を考える。
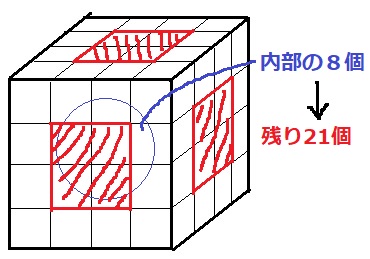
◆黒の面積の和が最も小さい場合
黒が表にでないようにする。
まず４×４×４の立方体の内部にある８個を黒にする。
残りの21個は、１面のみ現れる赤い斜線に配置。
本問の図には床が描かれていないので、底面の表面も塗られる。
４×６＝24面あるので、21個すべての黒を置くことができる。
１×21＝21ｃｍ2（ア）
◆黒の面積の和が最も大きい場合
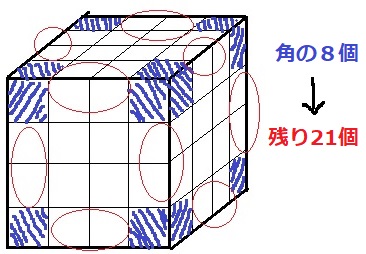
黒を目立たせる。
３面あらわれる角の８つに黒を優先的に配置。
残りの21個は２面あらわれる赤い〇のところ。
これは立方体の１辺に２つずつあるので、
２×12辺＝24個あるから、すべての黒を置くことができる。
３×８＋２×21＝66ｃｍ2（イ）
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント