2020年度　早稲田中学過去問【算数】大問３解説

問題ＰＤＦ
三角すいＡＢＣＤの頂点Ａに点Ｐがあり、点Ｐは１秒ごとに他の頂点に移動します。
たとえば、２秒後に点Ｐが頂点Ａにある移動の仕方は全部で３通りです。
次の問いに答えなさい。

（１）
３秒後に点Ｐが頂点Ａにある移動の仕方は全部で何通りですか。

（２）
４秒後に点Ｐが頂点Ａにある移動の仕方は全部で何通りですか。

（３）
５秒後に点Ｐが頂点Ａにある移動の仕方は全部で何通りですか。

（４）
９秒後に点Ｐが頂点Ａにある移動の仕方のうち、３秒後に頂点Ｂにあり、
６秒後に頂点Ａにある移動の仕方は全部で何通りありますか。

＠解説＠
（１）
１秒後、Ｂに行くとする。

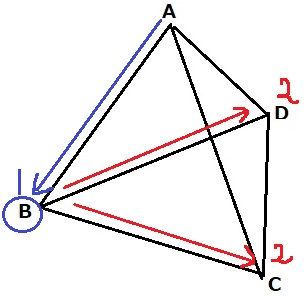
２秒後にＡへ向かうと、３秒後にＡへ戻らない。
横方向にＣかＤ、３秒後にＡに戻る→計２通り
１秒後にＣ・Ｄに行っても同様。
２×３＝６通り

（２）
Ａから下界にいくのは３通り。
下界での横方向は隣に行く→２通り

４秒間のルートを考える。最後は上（Ａ）に戻ってくること！
下→横→横→上…３×２×２＝12通り
下→上→下→上…３×３＝９通り
計12通り

（３）
５秒間のルートは、
下→横→横→横→上…３×２×２×２＝24通り
下→上→下→横→上…３×３×２＝18通り
下→横→上→下→上…さっきと同じで18通り
24＋18＋18＝60通り

（４）
Ａから３秒後にＢ。
下→上→下（Ｂ）…３通り
下→横→横…Ｂ→Ｃ→Ｂ、Ｂ→Ｄ→Ｂ、Ｃ→Ｄ→Ｂ、Ｄ→Ｃ→Ｂの４通り
計７通り

３秒後にＢからＡへ戻る。
正四角錘とすると、回転させても対称性から位置関係が同じ。
３秒後にＡ→Ｂで７通りなのだから、３秒後のＢ→Ａも同じ７通り

さらに３秒後のＡ→Ａは（１）で求めた通り、６通り。
したがって、７×７×６＝294通り
難関中（算数科）解説ページに戻る