2019年度　海陽中等教育学校過去問・特別給費【算数】大問３解説

問題ＰＤＦ
いくつかの点を平面上に配置することを考えます。３つの点であれば、図１のように正三角形の頂点上に配置することで、どの２点の距離も等しくできます。４つの点であれば、図２のように正方形の頂点上に配置することで、２点の距離は各辺の長さ（——-）と対角線の長さ（―――）の２種類にできます。

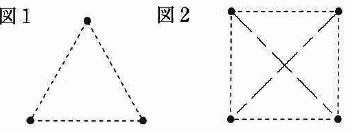
点の配置と、２点の間の距離について次の問いに答えなさい。ただし、図示するときには図２のように異なる長さは異なる種類の線で表すこと。

（１）
５点で距離の種類が２種類となっている配置を１つ図示しなさい。

（２）
図３のように直角二等辺三角形でない方の三角定規の頂点の位置に、３つの点配置しました。これに４点目を追加しても、距離の種類が増えないようにすることができます。たとえば図４の①の点です。４点目として他に考えられる点を２つ②、③として図示しなさい。

（３）
４点が距離の種類が２種類になるように配置したい。図２以外の配置を３つ図示しなさい。ただし回転したり、裏返したり拡大縮小して同じ形になるものは１つとします。

＠解説＠
距離を意識して点の配置を考える。面白い問題(*’ω’*)
解答は『異なる長さは異なる種類の線で表す』ことになっていますが、
以下の解説では頂点の位置のみ示しているところもあります。
（１）
５つの点を２種類の距離で配置する。
等距離を多く作る→円や正多角形を思い浮かべてみよう。

正五角形の一辺と対角線。
円の中心から72°ずつ離して配置する。

（２）
直角二等辺三角形ではない方の三角定規
⇒30°－60°―90°
最も短い辺の２倍が斜辺の長さになる。

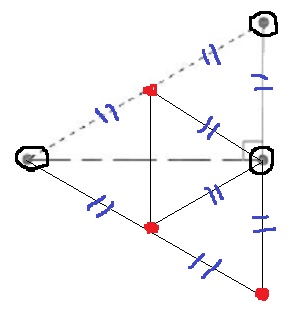
↑３つの赤い点のうち、２つを書けばいい。
それぞれの辺の長さは１：２：√３（←大きな正三角形の高さ）になる。

考えるコツとしては、どこかの頂点を中心にして、最も短い辺の半径に弧を描いてみる。
左か上の頂点を中心にして、最も長い斜辺を半径に弧を描いてみる。
２種類の正三角形が見えれば、正解に近づけるはず。

（３）
あれこれ想像しながら試行錯誤。
パズル問題のようで楽しい(ﾉ)`ω´(ヾ)

等距離をたくさん作るので、中途半端な図形にはならない。
対称図形だったり、正多角形や二等辺三角形など特徴的な図形になるはず。

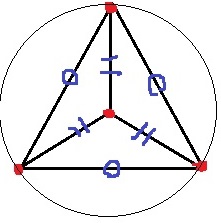
まず、３点を正三角形の頂点にする。
残りの１点を中心に置く。
ちょうど外接円の中心に来る。

前問で正三角形を利用したので、これを横に並べてみる。
この菱形の頂点も２種類の距離で離れている。

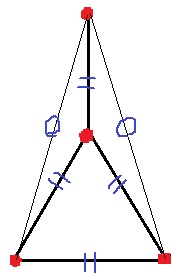
難しいが…正三角形の上部に、１辺の長さと同じ距離に４つ目の点を持っていく。
全体が30°－75°－75°の二等辺三角形になる。

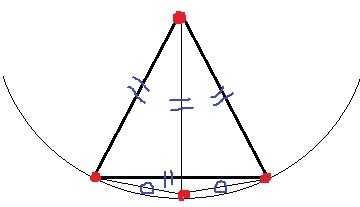
逆に、４点目を下へ持ってくることもできる。
正三角形の一番上の頂点を中心にコンパスで弧を描くと、
残り３つが円周上にくる。

（１）で答えた正五角形のうち、１つを除くと・・・。

時間をかければ２つは出てくるかもしれないが、
３つ出さなくてはならないのでツライ(´ﾟдﾟ｀)
難関中（算数科）解説ページに戻る