問題PDF
(1)
図のように、形の異なる平行四辺形が2つ重なっています。
角アの大きさは何度ですか。

(2)
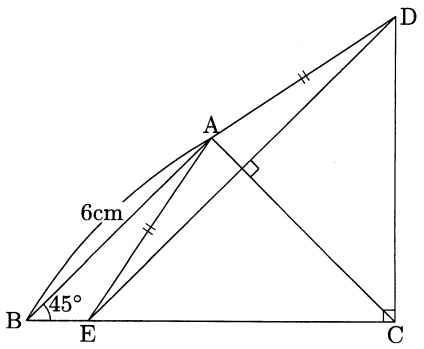
図の四角形ABCDの面積が33cm2のとき、三角形CDEの面積は何cm2ですか。
(3)
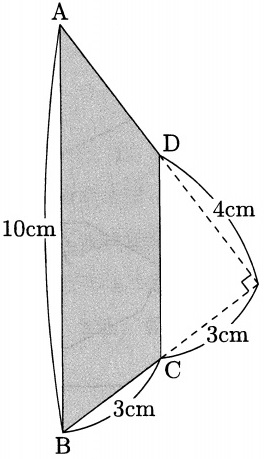
図の台形ABCDを辺ABを軸として1回転させてできる立体の体積は何cm3ですか。
@解説@
(1)

48°を錯角、19°を対頂角で移動。
右上の三角形で外角定理を使うと、平方四辺形の1つの内角は48-19=29°
これを同位角で左に移動。
ア=180-29=151°
(2)
ユニークな問題です。
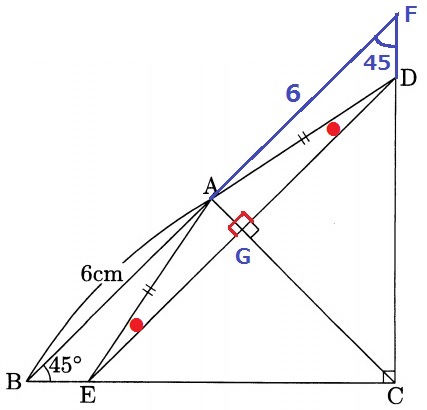
足りない部分を意識する。
BA、CDを延長、交点をFとする。
∠BFC=180-(45+90)=45°で、△CFBは直角二等辺三角形。
・・なんとなく、△ABEと△AFDが合同っぽい。
ACとDEの交点をGとする。
AGは二等辺三角形ADEを縦に真っ二つに分けるので、
AGを対称の軸とすると△ADGと△AEGは線対称で合同。
さらにいうと、AGを延長したACを対称の軸とすれば、
直角二等辺三角形CFB全体が左右対称に分かれる。
AF=AB=6cm
△CFBの面積…BF×BF÷2÷2=36cm2

△ADFの面積…△CFB-四角形ABCD=36-33=3cm2
対称性から△ACFと△ACBの面積が等しいので、
△ACDの面積…36÷2-3=15cm2
CD:DF=△ACD:△ADF=15:3=⑤:①
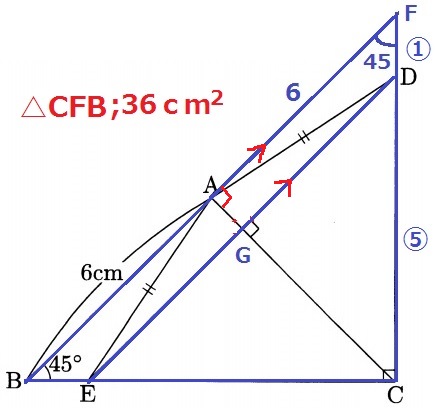
対称性で∠CAF=∠CAB=90°
∠CAF=CGD=90°で同位角が等しい。
BFとEDは平行で、△CFBと△CDEは相似。
△CFB:△CDEの辺の比は⑥:⑤、面積比は【36】:【25】
△CFBの面積が36cm2だから、△CDEは25cm2
(3)

△CDEは3:4:5の直角三角形。
●+×=90°で角度を調査すると相似図形が見つかる。
回転体の半径は、4×3/5=12/5cm

円柱の高さにあたるCDが5cmなので、円錐部分の高さの合計は5cm。
12/5×12/5×3.14×5+12/5×12/5×3.14×5×1/3
=12/5×12/5×3.14×5×(1+1/3)
=120.576cm3



コメント