問題ＰＤＦ
下の【図１】は１辺の長さが３ｃｍの正三角形を４つ組み合わせてできた三角すいで、
【図２】は、１辺の長さが１ｃｍの正三角形を４つと、
１辺の長さが１ｃｍの正六角形を４つ組み合わせてできる立体の展開図です。
あとの問いに答えなさい。
問１
【図２】を組み立ててできる立体の体積は、【図１】の三角すいの体積の何倍ですか。
問２
【図２】を組み立ててできる立体を、点Ａ、Ｂ、Ｃを通る平面で切り、
大きい立体と小さい立体に分けました。
このとき、（大きい立体の体積）：（小さい立体の体積）を、最も簡単な整数の比で表しなさい。
問３
問２で２つに分けた立体について、（大きい立体の表面積）：（小さい立体の表面積）を、
最も簡単な整数の比で表しなさい。
＠解説＠
問１
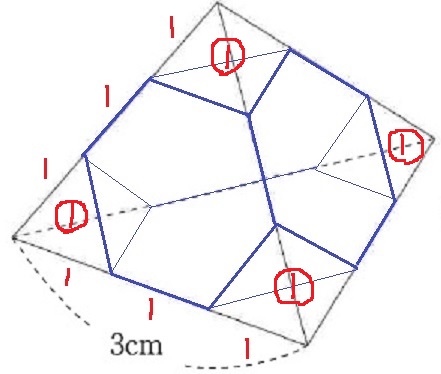
１辺３ｃｍの正三角錐の４つの頂点で、１辺１ｃｍの正三角錐を切り落とす。
すると、４つの正三角形、４つの正六角形で構成される八面体ができあがる。
１辺３ｃｍの正四角錘の体積を３×３×３＝27とすると、
うえの図形の体積は、27－１×１×１×４＝23
よって、23/27倍。
問２
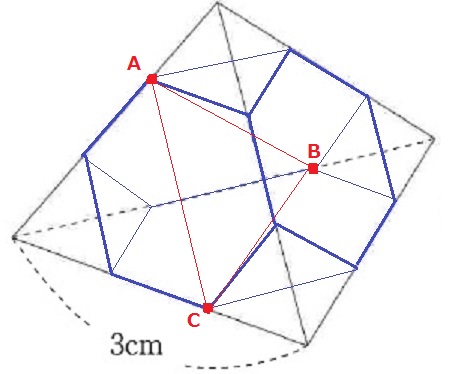
点の位置は正確に！
底面の正六角形でＢとＣ、側面の正六角形でＣとＡは対極にある。
Ａ・Ｂ・Ｃを通る断面は正三角形となる。
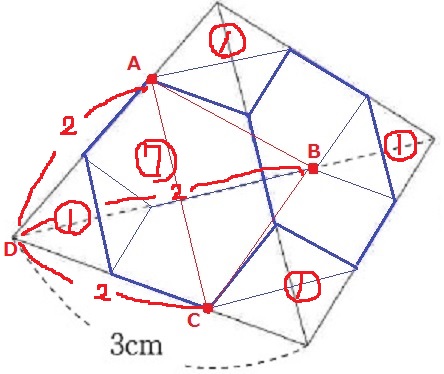
小さい立体の体積は、１辺２ｃｍの正四角錘ＡＢＣＤから①をひく。
小＝２×２×２－①＝⑦
大＝３×３×３－（①×４＋⑦）＝⑯
大：小＝16：７
問３
正三角形の個数を数えていく。
小＝１＋３×３＋４＝14
大＝１×３＋３×３＋４＋６＝22
大：小＝22：14＝11：７
難関中（算数科）解説ページに戻る
コメント