問題ＰＤＦ
点線で辺がかかれた正方形について、正方形の中に書かれた数字の本数だけ辺を線でなぞります。
たとえば、
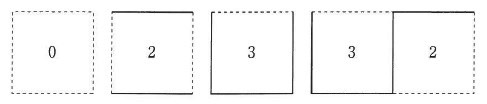
などのようになります。
（１）
となっているとき、辺のなぞり方は６通りあります。
６通りすべて答えなさい。
（２）
下の図において、辺のなぞり方がちょうど１通りとなるような（あ）と（い）の組合せをすべて答えなさい。
たとえば（あ）が３で（い）が２のときは、（３、２）のように答えること。
（３）
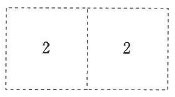
となっているとき、辺のなぞり方は何通りあるか答えなさい。
（４）
となっているとき、辺のなぞり方は何通りあるか答えなさい。
（５）
下の図において、（う）と（え）と（お）になぞることのできる数の組を入れる。
このような数の組をすべて考えると、辺のなぞり方は全部で何通りあるか答えなさい。
＠解説＠
（１）
どこかを固定して順次調べていく。
（２）
すべての辺を塗らない→（０、０）
すべての辺を塗る→（４、４）
４は１通りで決まる。
片方を４に固定すると、（あ）と（い）の境界線が塗られる。
他方を１にすると、境界線以外の３辺は必ず塗られない。
（４、１）（１、４）
０も１通りで決まる。
片方を０に固定すると、境界線が塗られない。
他方を３にすると、境界線以外の３辺は必ず塗られる。
（３、０）（０、３）
よって、（０、０）（３、０）（０、３）（４、１）（１、４）（４、４）
（３）
境界線の有無で場合分け。
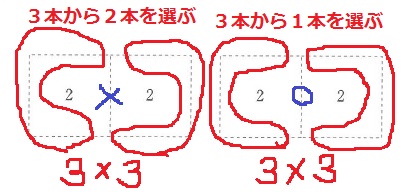
左は境界線が塗られない。
残りの３辺から２本選ぶので、左右で３×３＝９通り
右は境界線が塗られる。
残りの３辺から１本選ぶので、左右で３×３＝９通り
よって、９＋９＝18通り
（４）
数字の大きいところから確定していく。
４は全ての辺が塗られる。３で場合分け。
・左
１と３の境界線が塗られるので、１の正方形で残りの３辺が塗られない。
２の正方形で２通り。
・中央
同様に、１と３の境界線が塗られるので２通り。
・右
３の正方形の上は塗られない。
２で残る１辺は３通りに分かれる。
２＋２＋１＝５通り
したがって、２＋２＋５＝９通り
（５）
問われているのは（う）・（え）・（お）に入る数の組合せではなく、
辺のなぞり方は全部で何通りあるか。
今までと趣向は変わるが、実はシンプル。
各辺は塗られるか・塗られないかの２通り。
10辺あるので、２を10回かける。
２10＝1024通り
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント