問題ＰＤＦ
体積が180ｃｍ3の正四面体ＯＡＢＣがあり、
辺ＯＡ、辺ＯＢ、辺ＯＣの中点をそれぞれＰ、Ｑ、Ｒとします。
（１）
３点Ｐ、Ｂ、Ｃを含む平面と、３点Ｑ、Ａ、Ｃを含む平面の２つの平面でこの立体を切り分けるとき、頂点Ｏを含む立体について、（ア）面の数（イ）辺の本数（ウ）頂点の数（エ）体積をそれぞれ答えなさい。
（２）
３点Ｐ、Ｂ、Ｃを含む平面と、３点Ｑ、Ａ、Ｃを含む平面と、３点Ｒ、Ａ、Ｂを含む平面の３つの平面でこの立体を切り分けるとき、頂点Ｏを含む立体について、（オ）面の数（カ）辺の本数（キ）頂点の数（ク）体積をそれぞれ答えなさい。
＠解説＠
（１）
問題文に正四面体が描かれていない。。
↑こうなります。
下はくの字に曲がり、四角錘になる。
（ア）面の数…５面（イ）辺の本数…８本（ウ）頂点の数…５個
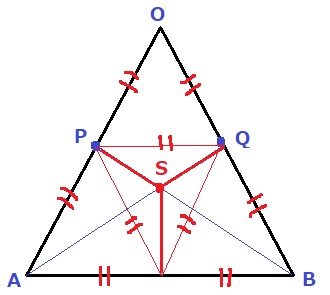
錘なので、底面を四角形ＯＰＳＱで捉える。
四角形ＯＰＳＱは正三角形ＯＡＢの３分の１。（合同図形が３つある）
（エ）体積…180÷３＝60ｃｍ3
（２）
さらに面ＲＡＢで切断。
きれいに描かないと訳が分からなくなる。
120°ずつ分かれた３方向から中央下に向かって同じ角度で切断するので、
立体の下は１点に交わり、それはＯの真下。
（オ）面の数…６面（カ）辺の本数…12本（キ）頂点の個数…８面
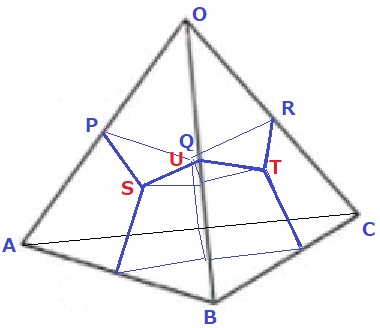
お分かり頂けるであろうか(;^ω^)
同じパーツを４つ作り、Ｏ・Ａ・Ｂ・Ｃ方向からパカッとはめ込むと正四面体ＯＡＢＣになる。
（ク）体積…180÷４＝45ｃｍ3
難関中（算数科）解説ページに戻る
コメント