問題PDF
下の図のように、マス目に以下の手順で記号〇、●を入れていきます。
・1番上の行のマス目にはすべて〇を入れる。
・1番左の列のマス目にはすべて〇を入れる。
・それ以外のマス目には、左のマス目と上のマス目に同じ記号が入っているときは●を、
異なる記号が入っているときは〇を入れる。
例えば、2行目2列目のマス目には、左のマス目にも上のマス目にも〇が入っているため、
●を入れます。
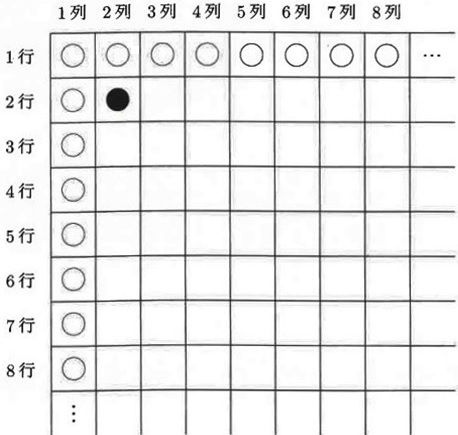
このとき、次の問いに答えなさい。
(1)
4行目4列目までの16個のマス目には〇と●がどのように入れられるか。
[解答欄]の空らんの部分に〇、●をかきなさい。

(2)
16行目16列目までの256個のマス目に〇と●を入れたとき、
その中に含まれる〇の個数を求めなさい。
(3)
[ あ ]行目[ あ ]列目までのマス目に〇と●を入れると、〇の個数が1000個以上になります。
[ あ ]にあてはまる数の中で、最も小さいものを求めなさい。
@解説@
(1)
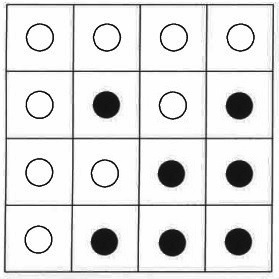
条件に従って埋めていく。上と左が同色で●になる。
ここを間違えると、うしろも解けないので慎重に!
(2)

いきなり16行目16列目はわからないので、問題文の8行目8列目まで埋めてみよう。
1行目と1列目はすべて〇。2行目2列目は〇と●が交互になる。
埋めていくと、5行目と5列目で〇がストレートに4つ並ぶ。
〇か●かは上と左に依存するので、〇が4連続する赤線を頼りに考えると、
(1)の4×4と同じ模様が現れる。
しかし、5行目5列目は●となり、右下の4×4だけは全部●になる。
同じ模様が右下以外の3ヶ所にできる。
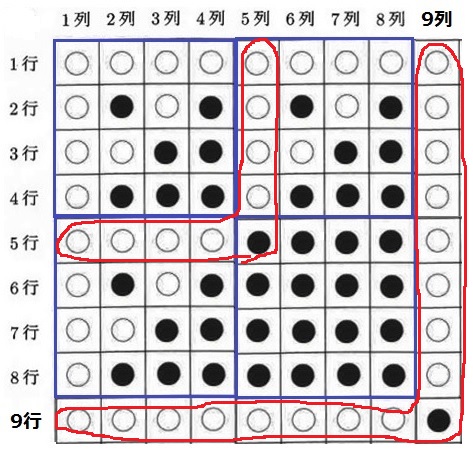
次の9行目9列目をやってみると、こんな感じになる。
〇がそろってリセットされるようで、5行目5列目と様相が似ている…。
8×8を1つの模様として、今度は右と下に同じ模様が、右下に黒だけが連なるのでは?

これを想像できるかどうか。
(1)の解答をよくみると、4×4の中でも2×2で区切ると同じ模様が浮かんでみえる。
16×16を試験会場で書くのはさすがに困難だが、
同じ模様が連続して現れる自己相似(フラクタル)だとすれば光が見えてくる。
同じ模様が3ヵ所出現⇒〇の数を3倍していく。
2×2…3個
4×4…3×3=9個
8×8…9×3=27個
16×16…27×3=81個
(3)
続きをやると、
32×32…81×3=243個
64×64…243×3=729個
次で1000を超えるので、1行1列ずつチェックしていく。

65行目65列目は右下以外すべて〇。(5行目5列目の様子を見るとわかりやすいかも)
729+64×2=857個
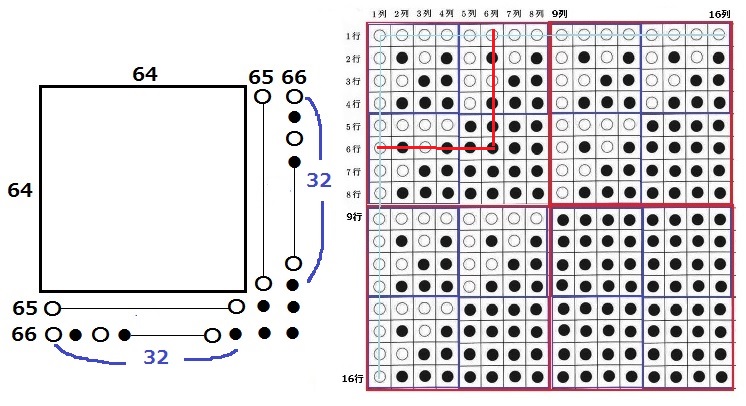
66行目66列目は〇●〇●…が続く。
4個中2個が〇→64÷2=32個が2つ分。
857+32×2=921個
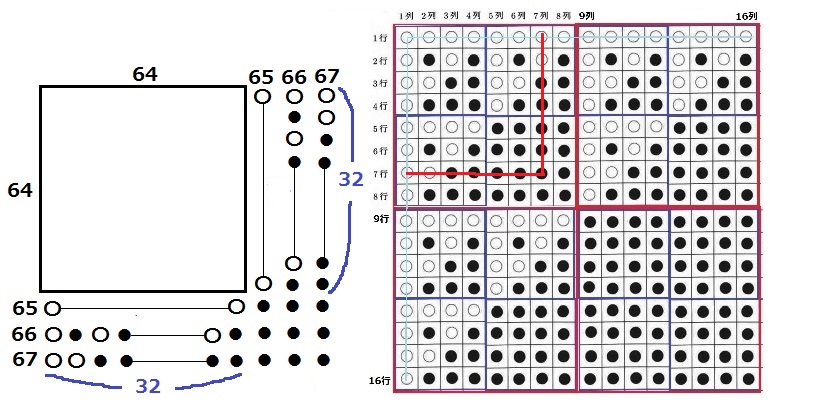
67行目67列目は〇〇●●…がつづく。
先ほどと同様に4個中2個なので、921+64=985個
68行目68列目は〇●●●…がつづく。
4個中1個なので、32÷2=16個が2つ分。
985+16×2=1017個
したがって、答えは68。
@余談@
本問は有名なフラクタル図形の亜種にあたる。

ガスコン研究所より。
頂点に1。以下、両端に1を置いて、左上と右上の数字の和を下に書いていく。
数学の世界では名の知れたパスカルの三角形で、奇数だけを塗りつぶすとフラクタルがあらわれる。

見たことある人いるんじゃないかな?
シェルピンスキーのギャスケットといいます。

市川の問題を斜めで見ると、左上部分がシェルピンスキーのギャスケットになります。
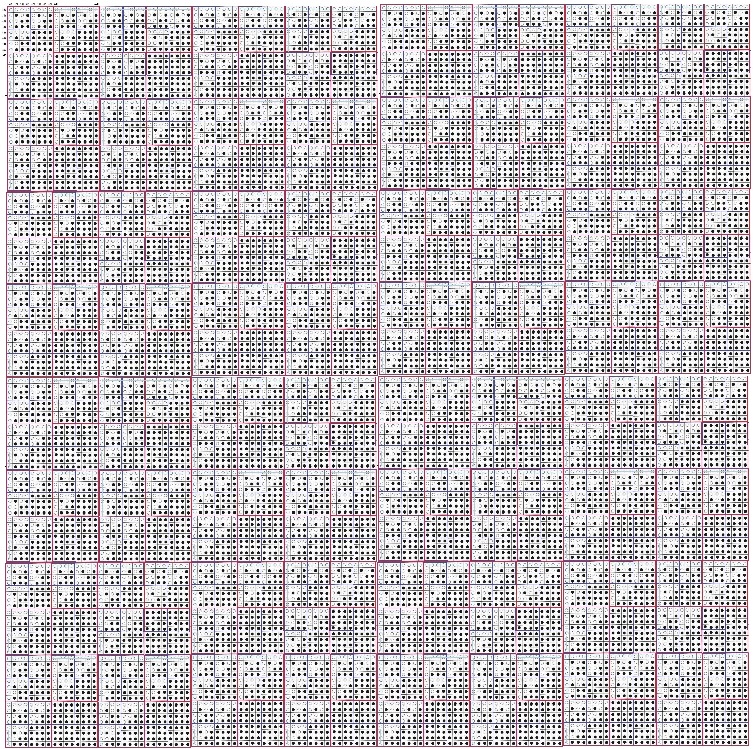
気持ち悪い(´°ω°`;)

シェルピンスキーは四面体もあります。
上図は四面体の内部の方に色が塗られています。
フラクタルってなんか人を不安にさせますね…。



コメント