問題PDF
図のような、点Oを中心としてABを直径とする円の周上を、点Pは時計回りに、点Qは反時計回りにそれぞれ一定の速さで動きます。2つの点はAを同時に出発し、点Pは点Qの4倍の速さで進みます。図の(あ)は、点QがAから動いたときの、円の半径OAとOQの間の角を表します。(あ)の大きさは、0度から360度までを考えるものとして、以下の問いに答えなさい。
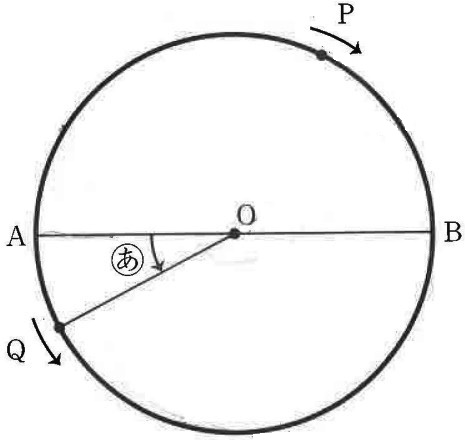
(1)
次の空欄ア、イに入る数を答えなさい。
2点P、QがAを同時に出発した後で、1回目に重なったときの(あ)の大きさは〔 ア 〕度です。その後、2点が何回か重なった後、初めてAで重なるのは、2点が〔 イ 〕回目に重なったときでした。
(2)
2点がAを同時に出発した後、初めてAで重なるまでに、点Pと点Qを結んでできる直線が、円の直径ABと平行になるときが2回あります。このときの(あ)の大きさを小さい順に答えなさい。ただし、直線PQが直径ABと重なるときは平行ではないとします。
(3)
2点がAを同時に出発した後、初めてAで重なるまでに、点Pと点Qを結んでできる直線が、円の直径ABと垂直になるときが2回あります。このときの(あ)の大きさを小さい順に答えなさい。
(4)
Aと(2)で求めた2か所の点Qの位置を結んでできる三角形の面積と、Aと(3)で求めた2か所の点Qの位置を結んでできる三角形の面積の比を最も簡単な整数の比で答えなさい。
@解説@
(1)
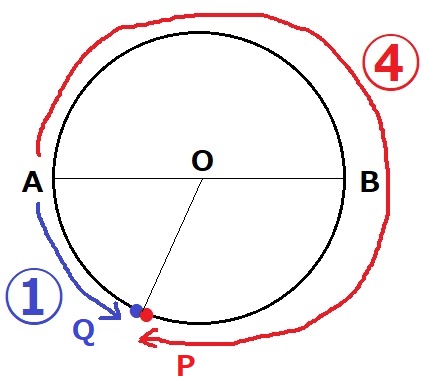
Pが進んだ距離を④とすると、Qの距離は①
∠AOQ=360×①/⑤=72°
2点が同じ場所からスタートして、Qが反時計回りに72°進むたびにPと出会う。
QがAに戻るまでにPと360÷72=5回出会い、5回目の出会いがちょうどA。
ア…72、イ…5
(2)
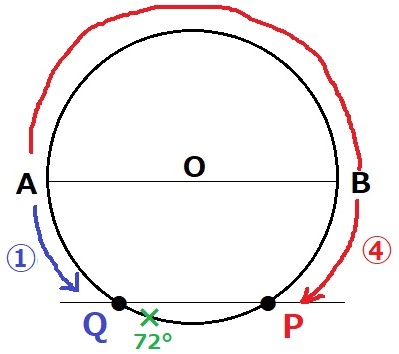
1回目の出会い(72°)よりも前で、ABとPQが平行になる。
だいたい上図のあたり。
AとB、PとQが対応するように線対称で分ける。
AQ=BP=①
半周の180°が③なので、∠AOQ=180×①/③=60°
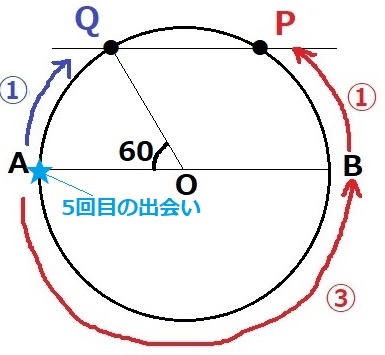
ABとPQが平行になるのは『2回』しかない。
5回目の出会いがAなので、ここから逆再生した場合も平行になる。
すなわち、Aから時計回りにQが①、反時計回りにPが④進んだ場所である。
求めるのは反対側の角だから、∠AOQ=360-60=300°
60°、300°
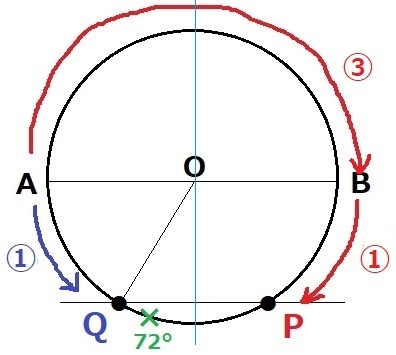
(3)
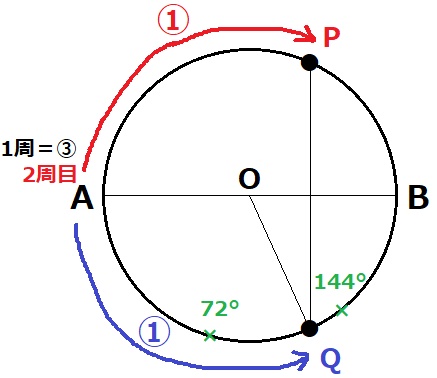
Pはいち早くBに到達して下半分に来てしまうので、
1周目ではABとPQは垂直にならない。
PとQが出会い、Pが2周目で再び上半分にきたときから2回目の出会いまでに垂直となる。
上下対称でAQ=AP=①
Pは④進むから、1周の長さは④-①=③
∠AOQ=360×①/③=120°
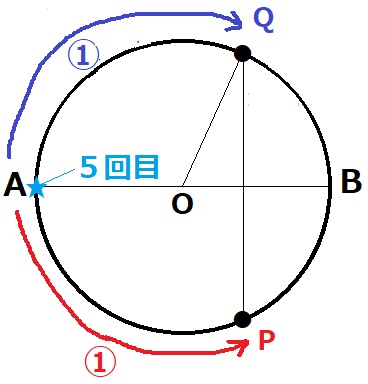
ここも垂直は『2回』だけだと情報提供してくれているので、
先ほどのようにゴールのAから逆再生する。
∠AOQ=360-120=240°
120°、240°
(4)
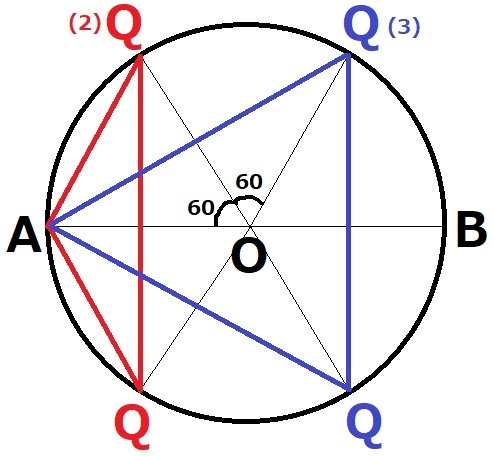
Qの位置を記す。
中心角をみると、A・B・Q×4個が円周を6等分している。
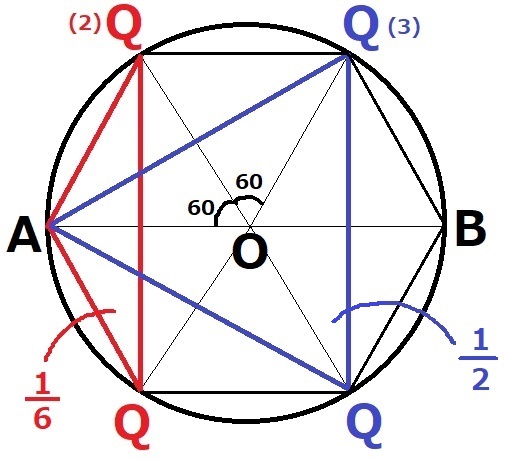
正六角形を描くと、典型的な分割が見える。
赤:青=1/6:1/2=1:3



コメント