2019年度　明治大学付属明治中学過去問【算数】大問３解説

問題ＰＤＦ
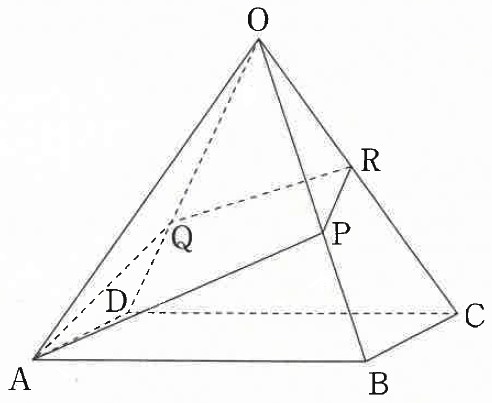
下の図のように、すべて辺の長さが10ｃｍの四角すいＯＡＢＣＤがあります。
辺ＯＢ、ＯＤをともに３：２に分ける点をそれぞれＰ、Ｑとします。
四角すいＯＡＢＣＤを３点Ａ、Ｐ、Ｑを通る平面で切ったとき、
その平面と辺ＯＣが交わる点をＲとします。

（１）
ＯＲの長さは何ｃｍですか。

（２）
四角すいＯＡＰＲＱの体積と四角すいＯＡＢＣＤの体積の比を、最も簡単な整数の比で表しなさい。
ただし、三角すい、四角すいの体積は（底面積）×（高さ）÷３で求められます。

＠解説＠
（１）
△ＯＡＣを正面に捉えると、ＰルートとＱルートが直線でかぶる。

メネラウスの定理を使う。
３/２×１/２×ＣＲ/ＲＯ＝１
ＣＲ：ＲＯ＝４：３
ＯＲ＝10×３/７＝30/７ｃｍ

＠別解＠
メネラウスを使わない場合はベンツ切りをする。

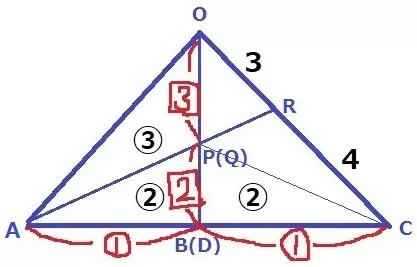
ＯＰ：ＰＢ＝３：２から、△ＡＯＰ：△ＡＰＢ＝③：②とする。
ＰＣに補助線。ＡＢ：ＢＣ＝１：１より、△ＡＰＢ＝△ＣＰＢ＝②
ＣＲ：ＲＯ＝△ＡＣＰ：△ＡＯＰ＝４：３

（２）
Ｏ－ＡＰＲＱを面ＯＰＱで２つに分割する。

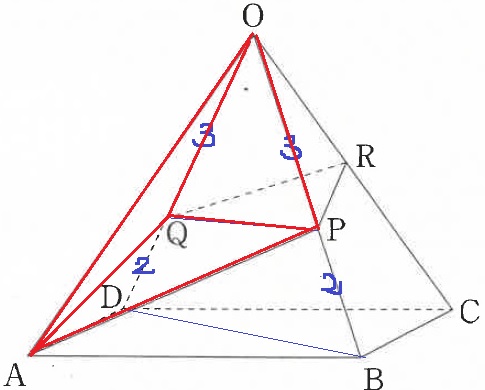
正四角錘Ｏ－ＡＢＣＤの体積を１とすると、Ａ－ＯＢＤはその半分。
Ａ－ＯＢＤ：Ａ－ＯＰＱ＝△ＯＢＤ：△ＯＰＱ＝25：９
Ａ－ＯＰＱ＝１×１/２×９/25＝９/50

Ｃ－ＯＢＤも全体の半分。
底面積の比→△ＯＢＤ：△ＯＰＱ＝25：９
高さの比→ＯＣ：ＯＲ＝７：３
Ｒ－ＯＰＱ＝１×１/２×９/25×３/７＝27/350
よって、Ｏ－ＡＰＲＱ＝９/50＋27/350＝９/35
難関中（算数科）解説ページに戻る