2019年度　西大和学園中学・県内過去問【算数】大問４解説

問題ＰＤＦ
長さが１ｍである９色の棒が１本ずつあります。
棒の色ごとに【表】のようにそれぞれの棒を等分します。

〔１〕同じ色の棒だけをつなげて、いろいろな長さの棒を作ることを考えます。
ただし、棒１本だけで作ってもよいものとします。
＜例＞
・黄色の棒１本だけで、長さが１/５ｍの棒を作ることができます。
・青色の棒を３本つなげると、長さが３/８ｍの棒を作ることができます。
・黄色の棒１本だけで作った棒の長さと、黒色の棒２本つなげて作った棒の長さは、
どちらも同じ１/５ｍです。
（１）
長さが１/２ｍの棒で、異なる色のものは全部で何本できますか。

（２）
次の〔　ア　〕～〔　ウ　〕に当てはまる数を答えなさい。
作ることのできる棒の長さは全部で〔　ア　〕通りあり、
15番目の長さは〔　イ　〕ｍとなります。
また、〔　ア　〕通りの長さをすべて足し合わせると〔　ウ　〕ｍとなります。

（３）
次の〔　エ　〕と〔　オ　〕に当てはまる色の組み合わせをすべて答えなさい。
ただし、〔　エ　〕と〔　オ　〕は異なる色とします。
〔　エ　〕の棒を２本つなげた棒の長さから、〔　オ　〕の棒１本の長さをひくと、
緑色の棒１本と同じ長さになります。

〔２〕さらに、異なる色の棒をつなげてもよいものとします。
＜例＞
・白色の棒１本と黒色の棒１本をつなげると、
長さが３/５ｍの棒を作ることができます。
・オレンジ色の棒２本と黄色の棒１本をつなげると、
長さが７/10ｍの棒を作ることができます。

（４）
棒をつなげて長さが２/３ｍの棒を作る方法を考えます。
２種類の色の棒を使う場合、全部で何通りの方法がありますか。
ただし、色の種類と棒の本数が同じものは、つなぐ順序に関係なく１通りと考えます。

（２）
ここらからきつくなってくる(´ﾟдﾟ｀)

分数になおしたとき、約分できる分数は長さがかぶってしまう。
たとえば、４/６は２/３に約分できるので、緑４本と赤２本は同じ長さ。
そこで、約分のできない既約分数を数える。
白…１/２
赤…１/３、２/３
ｵﾚﾝｼﾞ…１/４、３/４
黄…１/５、２/５、３/５、４/５
緑…１/６、５/６
水…１/７、２/７、３/７、４/７、５/７、６/７
青…１/８、３/８、５/８、７/８
紫…１/９、２/９、４/９、５/９、７/９、８/９
黒…１/10、３/10、７/10、９/10
これに１ｍをくわえて、32通り。
数が多くて面倒くさい(´Д｀)
ア…32

短い方から数えて15番目の棒の長さを求める。
自力でやると、途中で混乱する。
全体は32通りで、その半分は16番目。

ここで線分図をチラ見|дﾟ)
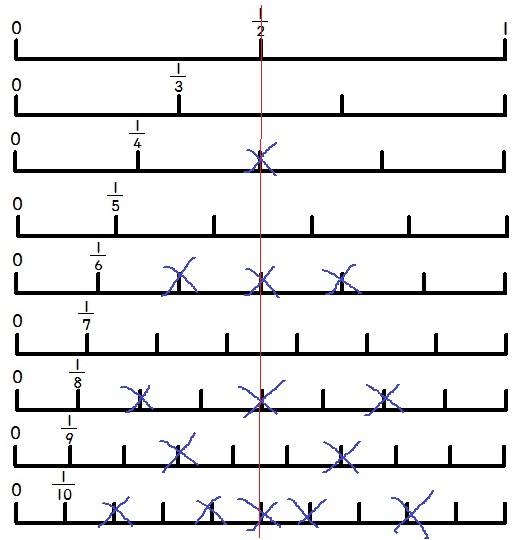
重複しているところは×。
32通りのうち、１ｍを除外した31通りに注目。
１/２のところで縦線をひくと左右対称になる。
つまり、１/２が半分の16番目で、それより下に15個、上に15個ある。
15番目は、１/２より下で１/２に近い数字になる。
（言い換えると、１/２未満の最大数）
分母が偶数だと約分で１/２となるから、その１個下は１/２から離れる。
奇数の分母に注目。
１/３、２/５、３/７、４/９（←分子を２倍しても分母に届かない）
この中で最も１/２に近いのは、分母の数が最も大きい４/９。
分母が大きければ大きいほど、目盛りの間隔は狭くなる。
イ…４/９

長さの合計を求める。
アで求めた既約分数の合計が答え。
分母と分子を同数にすれば１になる。
白…１/２⇒0.5ｍ
赤…１/３、２/３⇒１ｍ
ｵﾚﾝｼﾞ…１/４、３/４⇒１ｍ
黄…１/５、２/５、３/５、４/５⇒２ｍ
緑…１/６、５/６⇒１ｍ
水…１/７、２/７、３/７、４/７、５/７、６/７⇒３ｍ
青…１/８、３/８、５/８、７/８⇒２ｍ
紫…１/９、２/９、４/９、５/９、７/９、８/９⇒３ｍ
黒…１/10、３/10、７/10、９/10⇒２ｍ
同色の棒をすべてつないで１ｍ。
計16.5ｍ
ウ…16.5
通分は避けたほうが無難。

＠別解＠
１/２を真ん中として、下に15通り、上に15通りある。
左右対称なので、たとえば、２/５と３/５、２/９と７/９は対称関係にあり、
これらの和はそれぞれ１ｍである。
ということは、下15通りと上15通りを合わせると、１ｍの組合わせが15個できる。
１ｍ×15＝15ｍ
これに真ん中の１/２ｍと１ｍを足して、16.5ｍ。

（３）
式で表すと下のようになる。

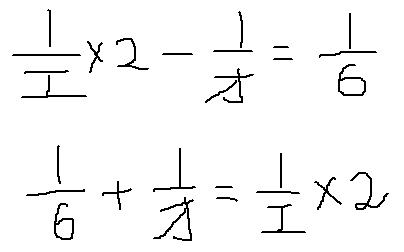
オに数字を代入して、８回調べる。
１/６＋１/２＝２/３
１/６＋１/３＝１/２
１/６＋１/４＝５/12
１/６＋１/５＝11/30
１/６＋１/７＝13/42
１/６＋１/８=７/24
１/６＋１/９＝５/18
１/６＋１/10＝４/15
このなかで、分母が10までの単位分数の２倍になるものは、
２/３⇒１/３×２、１/２⇒１/４×２のみ。
（エ、オ）＝（赤色、白色）（オレンジ色、赤色）

（４）
２つの和で２/３となる組み合わせを考える。
前問にでた〔１/２＋１/６〕が１つ。
もう１つは、〔１/３＋１/３〕。
基本の形はこれしかない。
ここらへん数的センスが問われる(；^ω^)

分母が大きいもの同士を倍にして帳尻を合わせれば２/３を作れそうだが、
実は作ることができない。
各単位分数を小数に直してみる。
１/２＝0.5
１/３＝0.333・・
１/４＝0.25
１/５＝0.2
１/６＝0.166・・
１/７＝0.142・・
１/８＝0.125
１/９＝0.111・・

２/３＝0.666・・の循環小数（無限小数）。
分母が７だと小数点以下が142・・のループで作れない。
分母が４、５、８は有限小数で、ここから0.666・・を作るには、
１/６に0.5を足すしかないので、結局は〔１/２＋１/６〕の形になる。
１/９を６倍すれば0.666・・だが、１種類の使用なので×。
分母が２・３・６の分数を使わずして、0.666・・を作る組み合わせはない。

＠１/２＋１/６＠
１/２＋１/６…白１本＋緑１本
２/４＋１/６…オレンジ２本＋緑１本
４/８＋１/６…青４本＋緑１本
５/10＋１/６…黒５本＋緑１本

＠１/３＋１/３＠
２/６＋１/３…緑２本＋赤１本
３/９＋１/３…紫３本＋赤１本
２/６＋３/９…緑２本＋紫３本
以上、７通り。
他に良い解法を見つけた方は、お問い合わせからお知らせ願います（＾＾;
難関中（算数科）解説ページに戻る