問題PDF
下の図のように8つの点A、B、C,D、E、F、G、Hが、円周を8等分しています。豊子さんと花子さんは最初に点Aにいます。豊子さんは反時計周り、花子さんは時計回りを自分の進む向きとして、2人がじゃんけんをして、次のようにこれらの8つの点を進むゲームをしました。
勝ったとき・・自分のいる点から自分の進む向きに2つだけ離れた点まで進む。
負けたとき・・自分のいる点から自分の進む向きとは逆の向きに1つだけ離れた点まで進む。
あいこのとき・・自分のいる点から自分の進む向きに1つだけ離れた点まで進む。
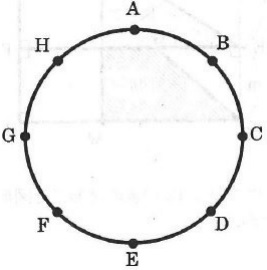
たとえば、1回目のじゃんけんで花子さんが勝った場合は、花子さんは点Cまで進み、豊子さんは点Bまで進みます。続けて、2回目のじゃんかんであいこであった場合は、花子さんは点Dまで進み、豊子さんは点Aまで進みます。このとき、次の各問いに答えなさい。
(1)
豊子さんと花子さんが点Aにいる状態から始めて、3回じゃんけんをしたところ、花子さんは点Hにいました。このとき、豊子さんはどの点にいますか。
(2)
豊子さんと花子さんが点Aにいる状態から始めて、3回じゃんけんをしたところ、花子さんは豊子さんのいる点から4つだけ離れた点にいました。このとき、あいこの回数は何回でしたか。
(3)
(1)の後、さらに3回じゃんけんをしたところ、豊子さんと花子さんは同じ点〔 〕にいました。〔 〕に当てはまる記号をA~Hの中からすべて答えなさい。
@解説@
(1)
ルールの確認。
自分の進行方向について、【勝ち…+2、負け…-1、あいこ…+1】
3回のじゃんけんで花子がスタート地点のAからHにきたということは、
2回負け、1回あいこで-1となった。
豊子は2回勝って1回あいこ⇒D
(2)
2人のあいだの差を考える。
花子が時計回り、豊子が反時計回り。
勝ち負けがつくと、2人は1離れる。
あいこがでると、2人は2離れる。
3回のじゃんけんで4離れたということは、あいこは1回でた。
(3)
(1)では花子がH、豊子がDにいる。
前問の考えを利用する。HとDは対極にあり、あいだの数は4つ。
3回のじゃんけんで4つを埋めるには、(2)と同様、あいこが1回あればいい。
1回のあいこで、花子はA、豊子はCにくる(あいだは2)
この状態から残り2回じゃんけんをする。
■花子が2回勝利
(A、C)⇒(C、D)⇒(E、E)
■豊子が2回勝利
(A、C)⇒(H、A)⇒(G、G)
■それぞれが1回ずつ勝利(勝った順を花→豊とする)
(A、C)⇒(C、D)⇒(B、B)
したがって、B・E・G



コメント