2018年度　学習院中等科過去問【算数】大問４解説

問題ＰＤＦ
下の図は半径が６ｃｍ、半径にはさまれた角度が42度のおうぎ形を点Ａを中心として回転したものです。
このとき、次の問いに答えなさい。

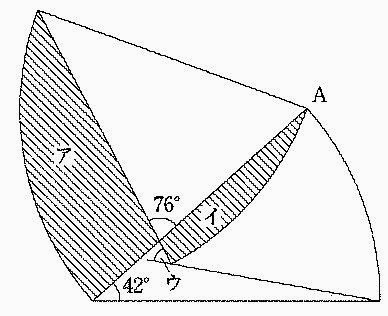
（１）
おうぎ形を何度回転させたか求めなさい。

（２）
斜線をつけた２つの部分アとイの面積の差を求めなさい。

（３）
角ウの大きさを求めなさい。

＠解説＠
（１）

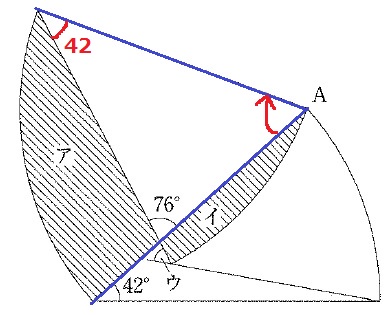
青い辺が回転した角度が、扇形が回転した角度。
180－（42＋76）＝62°

（２）

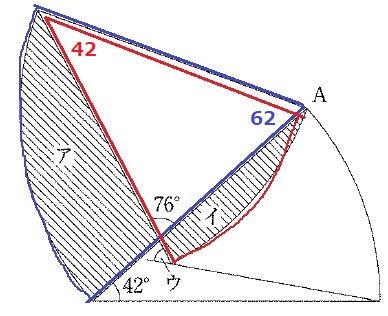
青い扇形から赤い扇形を引くと、共通部分の白い三角形が相殺されてア－イがでる。
６×６×3.14×62/360－６×6×3.14×42/360
＝６×６×3.14×20/360＝6.28ｃｍ²

（３）

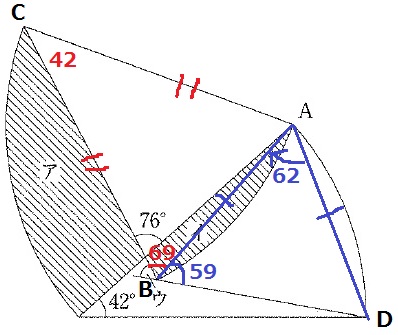
弦ＡＢ・ＡＤをつくる。
△ＡＢＣは半径が共通で二等辺→∠ＡＢＣ＝（180－42）÷２＝69°
△ＡＤＢは弦が共通で二等辺。さらに、∠ＤＡＢは図形の回転角度と同じ62°
→∠ＡＢＤ＝（180－62）÷２＝59°
∠ウ＝180－（69＋59）＝52°
難関中（算数科）解説ページに戻る