問題PDF
(図1)の三角形ABCは面積が98cm2の正三角形で、
BD:DC=CE:EA=AF:FB=3:4です。つぎの問いに答えなさい。

①
三角形CDEの面積は何cm2ですか。
②
さらに(図2)のように、AG=BG=CGとなる点Gをとります。
三角形GDHは正三角形です。角(あ)の大きさは何度ですか。
③
②で三角形DEFと三角形GDHの面積の比を最も簡単な整数の比で表しなさい。
④
②で三角形GDHの面積は何cm2ですか。
@解説@
①
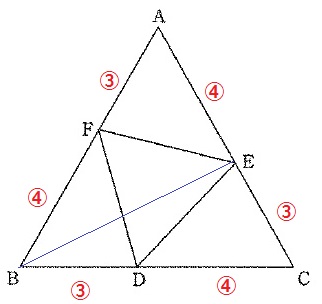
△ABC⇒△EBC⇒△CDE
98×3/7×4/7=24cm2
②
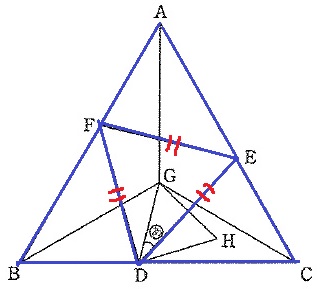
△AFEと△BDFと△CEDは、2辺とあいだの角が等しく合同。
DE=EF=EDで、△DEFは正三角形。
一方、AG=BG=CGから、△ABGと△BCGと△CAGは3辺が等しく合同の二等辺。
AG、BG、CGは正三角形ABCの3つの角の二等分線で、Gは重心(真ん中)に位置する。
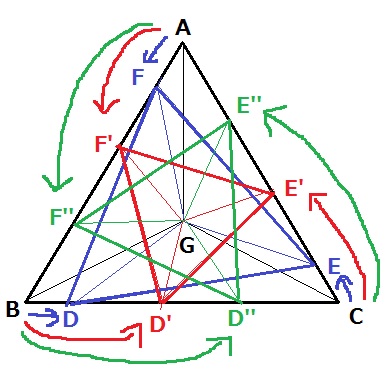
ここで、D・E・Fが各々B、C、Aから同じ速度で動く点だとする。
△AFEと△BDFと△CEDは合同なので、
BD=CE=AFの関係は維持され、△DEFは常に正三角形である。
そして、正三角形の真ん中(重心)も常にGにある。
D・E・Fを動かすとDG、EG、FGの長さは常に変化していくが、
3つの点は同じように動くので、外側(D側・E側・F側)の事情が変わってもGは動かない。
△ABCと△DEFは重心を共有し、DG=EG=FGが常に成り立つ。
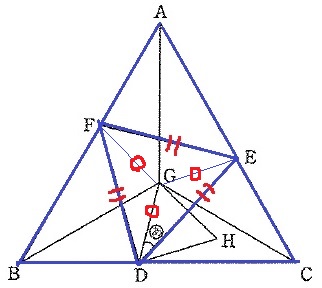
△GDEは二等辺で、∠DGE=360÷3=120°
(あ)=(180-120)÷2=30°
③
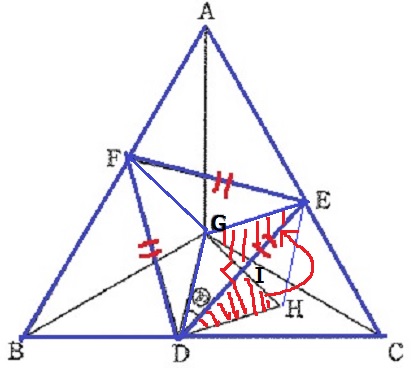
DEとHGの交点をIとする。
△GDHは正三角形で、△GDIと△HDIの内角は30°-60°-90°の直角三角形。
角度を調査すると△GEIの内角も同様で、DH=GD=GEより△DHIと△EGIは合同。
△DHIを△EGIに移植すると、正三角形GDHの面積は二等辺三角形GDEとなり、
二等辺GDEの面積は正三角形DEFの3分の1。
したがって、△DEF:△GDH=3:1
④
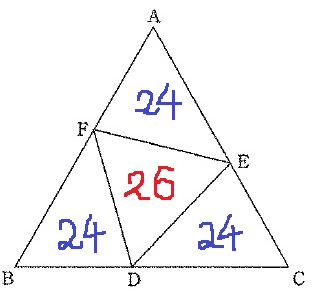
①で△CDE=24cm2と求めたので、
正三角形DEF=98-24×3=26cm3
③より、△GDHはこの3分の1だから、26÷3=26/3cm2
@余談;オイラー線@

外心O→三角形に外接する円の中心(3辺の垂直二等分線の交点)
重心G→頂点から対辺を中点を結んだ線(中線)の交点
垂心H→頂点から対辺に向けておろした垂線の交点
1つの三角形の3点O・G・Hは一直線上にあり、OG:GH=1:2の関係が成立する。
この直線はオイラー線とよばれ、以下のリンク先に詳しい証明が記述されております。
高校数学の美しい物語
三角形の五心ではベクトルをつかった証明法が多数あがっているので、
高校にあがって習ったらチャレンジしてみて下さい。
ちなみに、正三角形は外心・重心・垂心が一致するので、オイラー線がない!
内接円の中心である内心も一致する。



コメント