問題PDF
次の【 ア 】~【 オ 】にあてはまる数を答えなさい。
(1)
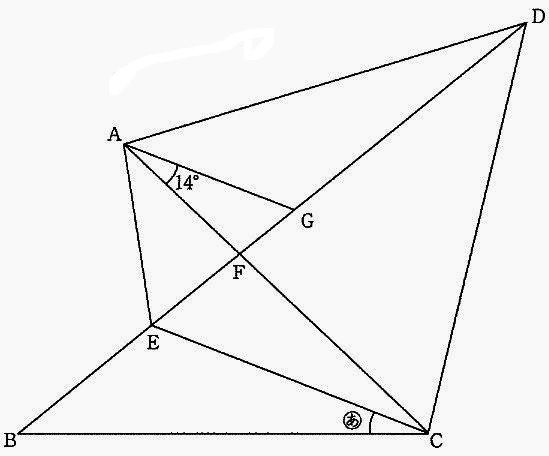
図において、三角形AEGと三角形ACDは正三角形で、
三角形FBCはFB=FCの二等辺三角形です。
図の角(あ)の大きさは【 ア 】度です。
(2)
図において、OCの長さは【 イ 】cmです。
また、(三角形OABの面積):(三角形ODEの面積)を
最も簡単な整数の比で表すと、【 ウ 】:【 エ 】です。

(3)
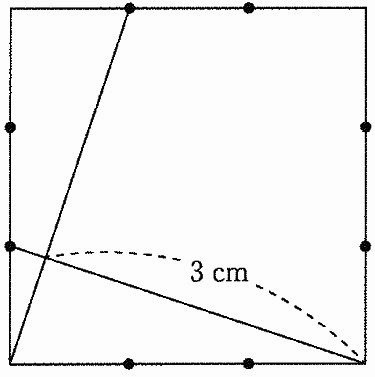
図において、●は正方形の各辺を3等分します。
このとき、正方形の面積は【 オ 】cm2です。
@解説@
(1)
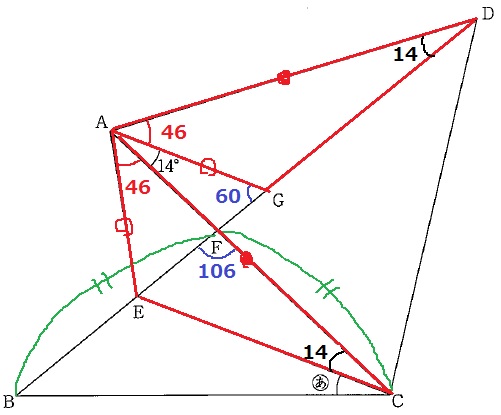
ポイントは△AECと△AGDの合同。
2つの正三角形の辺と、∠CAE=∠DAG=60-14=46°
2辺とあいだの角が等しいので合同になる。
△AGDで外角定理→∠ADG=60-46=14°
合同から、∠ACE=14°
△AFGの内角の和→対頂角で、∠BFC=180-(14+60)=106°
△FBCは二等辺三角形。
(あ)=(180-106)÷2-14=23°…ア
(2)
むずかしい:;(∩´_`∩);:
OCの長さが誘導になっている。
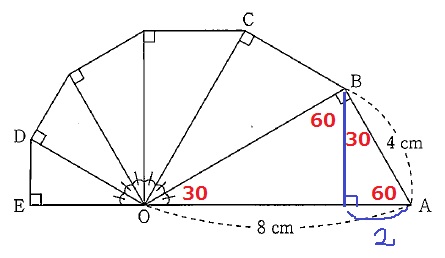
直角三角形は相似の宝庫!
∠BOA=180÷6=30°
30°-60°-90°の直角三角形が複数みつかる。
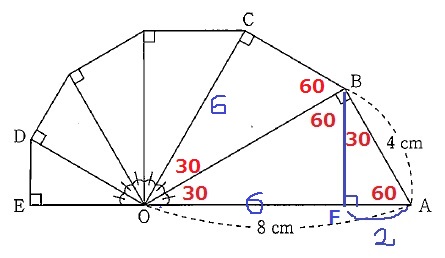
Bからの垂線とOAの交点をFとすると、AF=4÷2=2cm
OF=8-2=6cm
△BOFと△BOCは、斜辺を共有するので、
直角三角形の合同条件である斜辺と1鋭角から合同。
よって、OC=6cm…イ
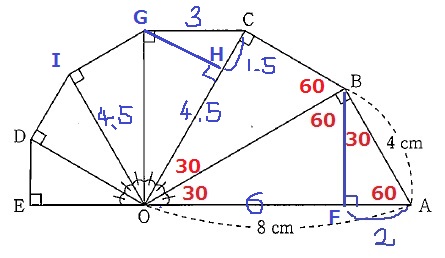
同様の手順で左に向かう。
CG=6÷2=3cm
Gから垂線、交点をHとすると、HC=3÷2=1.5cm
OH=6-1.5=4.5cm
GOを挟んで2つの合同な直角三角形から、IO=4.5cm

DI=4.5÷2=2.25cm
Dから垂線、交点をJとする。
IJ=2.25÷2=1.125cm
JO=4.5-1.125=3.375cm
DOを挟んで合同→EO=3.375cm
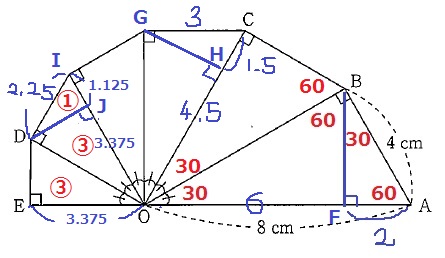
数値が酷いことに…。
ここからも難所。
△ODEは△OABと異なり、斜辺の長さがわかっていない。
そこで、△OIDを経由する。
IJ:JO=1.125:3.375=1:3
△DIJ=①、△OID=③。△ODE=③
△OABと△OIDの相似比は斜辺の長さから、
OA:OI=8:4.5=16:9
面積比は相似比の2乗。
△OAB:△OID=256:81
△OID:△ODE=④:③だから、
△ODE=81×3/4=243/4
したがって、△OAB:△ODE=256:243/4=1024:243
1024…ウ、243…エ
(3)
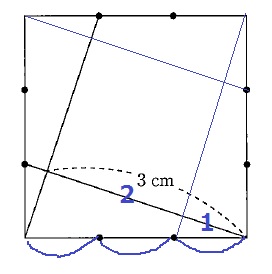
正方形をカット。2組の平行線ができる。
相似比から2:1⇒3cmを2cmと1cmに分割する。
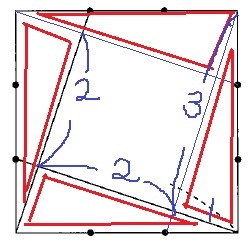
外側に4つの合同な直角三角形、中心に正方形。
1×3÷2×4+2×2=10cm2



コメント