2018年度　雙葉中学過去問【算数】大問４解説

問題ＰＤＦ
ある時計は３時20分から、長針も短針も進む速さは変わらずに、
長針だけが反対向きに進むようになってしまいました。
（１）
３時20分以降で、初めて長針と短針が重なるとき、正しい時刻は何時何分ですか。

（２）
３時30分以降で、短針が７と８の間にあって、長針と短針のつくる角が90度になるとき、
正しい時刻は７時何分ですか。すべて答えましょう。

（３）
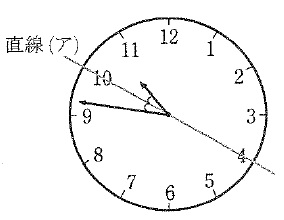
３時20分以降で、短針が10と11の間にあって、下の図のように長針と短針のつくる角が直線（ア）によって２等分されるとき、正しい時刻は10時何分ですか。

＠解説＠
（１）
３時20分の長針・短針の位置を確認。

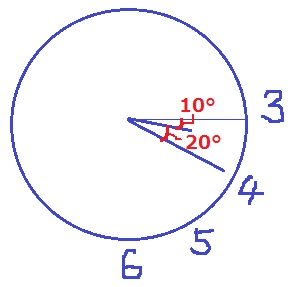
短針は１時間で30°動くので、20分間に30°×20/30＝10°動く。
３時20分では、長針と短針は20°離れていたことになる。

この状態から１分あたり長針は６°、短針は0.5°進み、両者は出会いにいくので、
20÷（６＋0.5）＝40/13＝３・１/13分後に重なる。
正しい時刻でいえば、３時20分＋３・１/13分＝３時23・１/13分

（２）
長針が向きを変えて、初めて12時に戻るのは３時40分。

このとき、短針は時計回りにまわるので、３時から20°のところにいる。
この４時間後である７時40分では、長針は12時を指し、短針は７時から20°のところ。
（長針が12時であれば、短針は＋20°）

両者は130°離れており、毎分６＋0.5＝6.5°ずつ接近する。
あいだの角が直角になるのは、長針・短針合わせて130－90＝40°進めばよいので、
40÷6.5＝６・２/13分後
７時40分＋６・２/13分＝７時46・２/13分

もう１つの直角は、７時46分・２/13分から180°（一直線）前に動いた状態。
180÷6.5＝27・９/13分前となる。
７時46・２/13分－27・９/13分
＝７時45・15/13分－27・９/13
＝７時18・６/13分
答え： 18・６/13分と46・２/13分

（３）
直線アが角の二等分線となる。
長針の動いた角度と短針の動いた角度から等角を導く式をつくり、
それぞれを左辺と右辺に配置して等式を立てる。

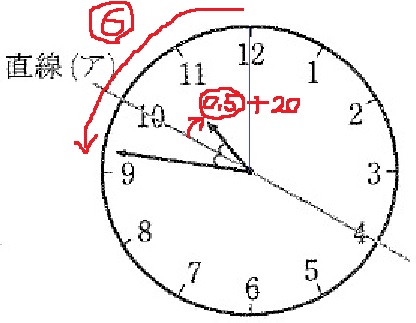
１分あたり、長針は⑥、短針は○0.5の距離を進む。
長針が12時を指したとき、すなわち、10時40分から考えよう。
長針の等角…⑥－60°
短針の等角…長針が12時を指すとき、短針は10時から20°動いたところにいる！
○0.5＋20°

⑥－60＝○0.5＋20
①＝80÷5.5＝14・６/11分
長針が12時を指した10時40分から14・６/11分後が答え。
40＋14・６/11＝54・６/11分

＠別解＠

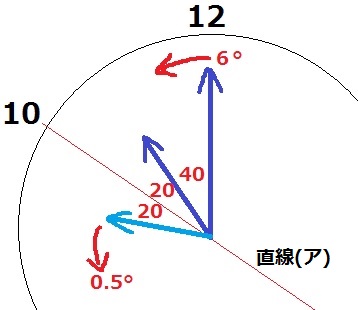
10時40分のとき、直線（ア）を対称軸として短針を移す。
この短針のシャドーは短針と対称的に動き、反時計回りに0.5°動く。
これと長針と重なったとき、長身と短針のあいだの角の二等分線が直線（ア）と符合する。
（40＋20＋20）÷（６－0.5）＝14・６/11分後
10時40分から14・６/11分後→10時54・６/11分
難関中（算数科）解説ページに戻る