2018年度　攻玉社中学過去問【算数】大問４解説

問題ＰＤＦ
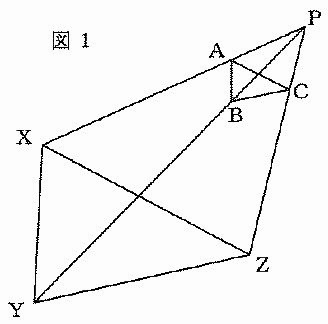
図１について、三角形ＡＢＣと三角形ＸＹＺのそれぞれの辺、ＡＢとＸＹ、ＢＣとＹＺ、ＣＡとＺＸは平行です。ＡＢ＝４ｃｍ、ＸＹ＝14ｃｍです。また、ＸＡ、ＹＢ、ＺＣを延長した線が交わる点をＰとします。

（１）
ＰＣ＝３ｃｍのとき、ＣＺの長さを求めなさい。

（２）
ＡＣとＢＰが交わる点をＱとします。
ＢＱ：ＱＰ＝１：３のとき、三角形ＸＹＺと三角形ＸＰＺの面積の比を求めなさい。

（３）
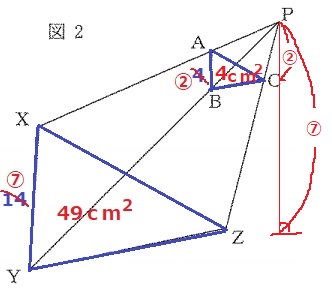
次に、図２のような三角すいを考えます。

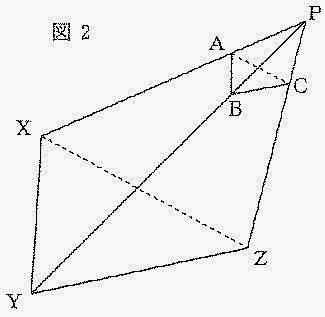
ＰＡ：ＡＸ、ＰＢ：ＢＹ、ＰＣ：ＣＺの比は等しいです。
ＡＢ＝４ｃｍ、ＸＹ＝14ｃｍ、点Ｐから三角形ＸＹＺまでの高さを12ｃｍ、
三角形ＸＹＺの面積を49ｃｍ²とします。
①
三角形ＡＢＣの面積を求めなさい。

②
三角すいＰＡＢＣの体積を求めなさい。

③
さらに、図３のような、三角形ＸＹＺを底面とする三角柱を考えます。
点Ｐがこの三角柱の上の面の辺にそって動くと、それにあわせて三角すいも形が変わるものとします。
点Ｐが上の面の三角形の辺にそって１周するとき、三角形ＡＢＣが通った部分の面積を求めなさい。

＠解説＠
（１）

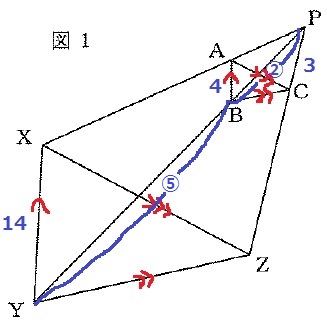
ＡＢとＸＹが平行→△ＰＡＢと△ＰＸＹが相似。
ＰＢ：ＢＹ＝４：14－４＝②：⑤
同様に、△ＰＢＣと△ＰＹＺも相似。
ＰＣ：ＣＺ＝ＰＢ：ＢＹ＝②：⑤より、ＣＺ＝３×⑤/②＝15/２ｃｍ

（２）

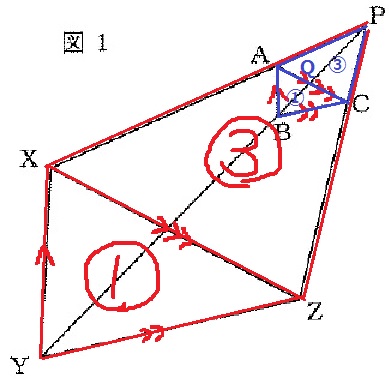
△ＡＢＣと△ＡＰＣにおいて、底辺をＡＣとすると高さの比はＢＱ：ＱＰ＝１：３
→△ＡＢＣと△ＡＰＣの面積比は１：３。

△ＰＡＣと△ＰＸＺは相似（③←→③）
さらに、△ＰＡＢと△ＰＸＹ、△ＰＢＣと△ＰＹＺも相似なので、
ＡＢ：ＸＹ＝ＢＣ：ＹＺ＝ＡＣ：ＸＺで３辺の比が等しく、
△ＡＢＣと△ＸＹＺが相似（①←→①）
ということは…△ＡＢＣ：△ＡＰＣ＝△ＸＹＺ：△ＸＰＺ＝１：３
（２つの三角形を合わせて、四角形ＡＢＣＰと四角形ＸＹＺＰが相似と捉えてもＯＫ）

（３）①
空間図形にチェンジ(σ･Д･)σ

ＰＡ：ＡＸ＝ＰＢ：ＢＹ＝ＰＣ：ＣＺから、三角錐Ｐ－ＡＢＣと三角錘Ｐ－ＸＹＺは相似。
底面積の△ＡＢＣと△ＸＹＺも相似。
相似比は４：14＝２：７
面積比は２×２：７×７＝４：49
△ＡＢＣの面積は、49×４/49＝４ｃｍ²

②

底面積がわかったので高さを求める。
高さの比も２：７だから、12×２/７＝24/７ｃｍ
三角錐Ｐ－ＡＢＣの体積は、４×24/７÷３＝32/７ｃｍ³

③

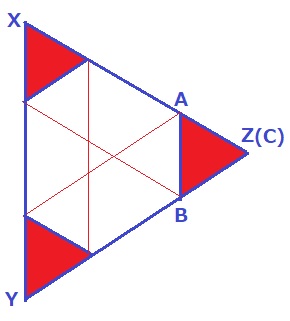
三角柱を上から眺める。
△ＡＢＣを△ＸＹＺの内壁に沿って平行移動させる。
平行線を描くと、真ん中の部分が通過しない場所。
全体（49ｃｍ²）から真ん中の部分を引けばいい。

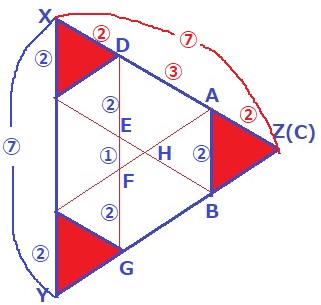
ＸＹ方面の比を〇、ＸＺ方面の比を〇とする。
ＸＤ＝ＡＺ＝②だから、ＤＡ＝③
ＤＺ＝⑤より、ＤＧ＝⑤
平行線からＤＥ＝ＦＧ＝②だから、ＥＦ＝①
△ＸＹＺ：△ＥＦＨ＝⑦×⑦：①×①＝49：１
△ＸＹＺは49ｃｍ²なので、△ＥＦＨを除いた部分の面積は48ｃｍ²
難関中（算数科）解説ページに戻る