2019年度　鹿児島県公立高校入試問題過去問【数学】解説

平均38.2点

問題はコチラ→ＰＤＦファイル

大問１（小問集合）－71.8％

（１）①　94.4％
５×（６－２）
＝５×４＝20　　　

②　90.6％
１/４＋５/３÷10/９
＝７/４

③　74.7％
２√７－√20＋√５－７/√７
＝２√７－２√５＋√５－√７
＝√７－√５

④　59.7％
２未満を選ぶ。
２は含まないので○。ウ

⑤　76.8％
ｘ＝４を代入して、等式が成り立つかを調べる。
ア・エ

（２）　75.8％

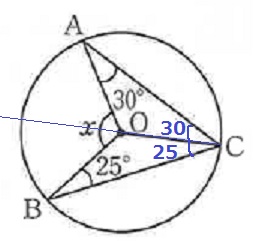
上と下の三角形で外角定理。
ｘ＝（30＋25）×２＝110°

（３）　65.3％
最小値　ｘ＝３のとき、ｙ＝９
最大値　ｘ＝６のとき、ｙ＝36
変化の割合…（36－９）/（６－３）＝９

*ｙ＝ａｘ²のグラフであれば、ｘの値がｐからｑと増加するときの変化の割合はａ（ｐ＋ｑ）。
１（３＋６）＝９

（４）　62.0％
高さが等しいので、円柱の体積の比は底面積の比。
円の面積は半径の２乗。
Ａ：Ｂ＝２²：１²＝４：１
ＡはＢの４倍。

（５）　46.7％
オクラって鹿児島が１位なんだね(ﾟДﾟ)
高知　…1733ｔ　－　14.2％
鹿児島…5153ｔ　－　？％
基準となる高知を分母に据える。
【14.2×5153/1733】　→　イ

大問２（小問集合２）－35.9％

（１）　25.1％！
ｙ＝－１/２ｘ²に放り込む。
Ａ（－２、－２）　Ｂ（４、－８）

ＡＢの傾きを求める。
Ａ→Ｂ。右に６、下に－６。
傾きは、－６/６＝－１

ＯＰは△ＯＡＢを２等分する
→ＰはＡＢの中点にある。（辺ＡＢを底辺してそれを２等分）
Ｐのｘ座標は、－２と４の真ん中。⇒１
傾きは１だから、Ａから右に３、下に３なので、Ｐ（１、－５）

（２）　57.6％
結果が１/３となる事象を求める。
全体は、₄Ｃ₂＝６通り
確率が１/３なので、結果が２通りになる和を調べる。
２枚の和は、３・４・５・５・６・７。
空欄に入る数は５となる。

（３）　28.0％！
結果を描いてみよう。
折り目はＢＣと平行。ＡがＢＣ上に重なる点がＤ。

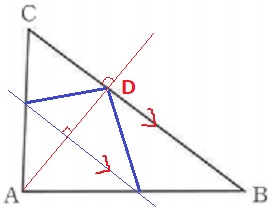
折り目は対称の軸で、点Ａと点Ｄは対応する。
対応する点を結んだ線分と、対称の軸は直角に交わる。
平行で同位角は等しいから、ＢＣとＡＤは垂直の関係。
①Ａを通り、ＢＣに垂直な線分を引く。
②ＢＣとの交点がＤ。
③ＡＤの垂直二等分線が折り目。

（４）　27.9％！
△ＡＢＰ≡△ＣＡＱの証明。

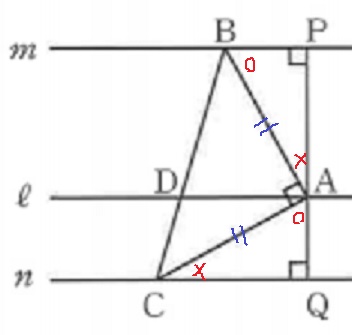
△ＡＢＣは直角二等辺三角形。
直角三角形の合同条件である、斜辺と１鋭角が等しい点を指摘する。
角度は、〇＋×＝90°で調べていく。

（５）　43.6％
連立方程式。計算過程も示す。
120円のリンゴをｘ個、100円のリンゴをｙ個とする。
80円のリンゴは３ｘ個。
３ｘ＋ｘ＋ｙ＝17
４ｘ＋ｙ＝17　…①

３ｘ×80＋120ｘ＋100ｙ＝1580
360ｘ＋100ｙ＝1580
36ｘ＋10ｙ＝158　…②

①②を解いて、ｘ＝３、ｙ＝５
80円のりんご…９個、100円のりんご…５個、120円のりんご…３個

大問３（データの活用）－23.9％

（１）　42.1％
範囲（レンジ）＝最大値－最小値＝10－２＝８点

（２）　22.3％！
５点以上の人数に注目。
ゲームは２回で、１回のゲームの得点は０、１、３、５点のいずれか。
５点（１人）…０＋５
６点（４人）…問題文より２人は３＋３だから、残り２人は１＋５。
８点（２人）…３＋５
10点（１人）…５＋５
１回でも５点を得たのは６人。

（３）①　11.5％！
１点と５点をチェンジする。
20人のメジアンなので、10番目と11番目の平均値が答えとなる。
得点の高い順から探っていった方がいい。

１番得点が高いのは、１＋１＝２点
５＋５＝10点となり、この５人がベスト５。
次に高いのは、１＋３＝４点
５＋３＝８点となり、ここまでがベスト10。
11位は、５＋１か３＋３＝６点。
いずれであっても６点のまま。
６点と８点の平均で、答えは７点。

②　23.9％！
すべて式の正誤判定。
問題文の条件から何が新しく言えるのかを考える。

20人のメジアンが5.5点→10番目が５点、11番目が６点（Ｂ）。
Ａは４点、６点はＢのみ。

ア：レンジは最大値－最小値。
メジアンしか判明しておらず、最大値、最小値の情報はわからない。×
イ：点数の低い順で、11番目以降の10人は６点以上。
６点はＢ１人なので、８点と10点は合計９人いる。
10番目の５点と８点と10点は、５点の部分に必ず入れなければならないので、
１回でも５点にボールを止めた人は少なくとも10人はいる。
前のゲームで、５点、８点、10点は、表から合計４人しかいない。
この４人すべてが１ゲームで５点を入れたとしても、
最低６人が２ゲームで５点に入れたことになる。
よって、１ゲーム目より２ゲーム目の方が５点に止めた人数が多い。○
ウ：最頻値の情報なし。×
エ：11番目以上の10人は６点以上。５点が１人いる。
よって、４点のＡを上回っている生徒は11人いる。○

大問４（整数）－23.9％

（１）　47.1％
ある数から左上にいくと、ある数－10になっている。
問題文の枠の中で言えば、15－10＝５。
ａ＝ｘ－10

（２）①　25.6％！
同様に、ｂ＝ｘ－８、ｃ＝ｘ＋８、ｄ＝ｘ＋10とおいて計算するだけ。
Ｍ＝ｂｄ－ａｃ＝（ｘ－８）（ｘ＋10）－（ｘ－10）（ｘ＋８）
＝ｘ²＋２ｘ－80－ｘ²＋２ｘ＋80＝４ｘ
ｘは自然数なので、Ｍは４の倍数。

②　10.9％！
前問より、Ｍ＝４ｘ
Ｍの１の位が４となるｘを求めたい。
ｘ＝１のとき、４×１＝４
ｘ＝６のとき、４×６＝24
４の倍数で１の位が４になる組み合わせはこれしかない。
ｘ＝１、６
ア…１　イ…６

ａが１～10段目なので、ｘは２段目～11段目まである。
この範囲のなかで、１の位が１と６の数字の個数を求める。

１の位が１の数字だけ見てみよう。
１、11、21、31、41・・と右下に向かって斜めに並んでいる。
一番右の列は９の倍数が並び、その９段目は９×９＝81。
10段目は82～90と１の位が１の数字はなく、11段目の左に91が表れる。
留意すべきは、ｘは３×３の枠に囲まれた９つの数字の中央にある数字なので、
一番上の１段目は除外。さらに、一番右と左の列も除外すること。
該当する数字は、11～71の７つ。

１の位が６も同様。
16、26、56～96で、７つ。
よって、７＋７＝14通り
ウ…14
丁寧に認定すること！

大問５（図形）－25.7％

（１）
正八面体にまつわる設問。
正八面体の辺の数は12本。
立体図から数える。ア…12　（62.2％）

正方形ＢＣＤＥの面積。
対角線の長さは４ｃｍ。正方形の面積＝対角線×対角線÷２
４×４÷２＝８ｃｍ²　イ…８　（37.6％）

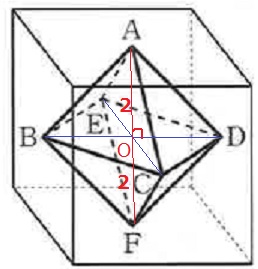
ＢＤとＥＣの交点をＯとする。
Ｏは正方形と正八面体の中心にある。
ＡＦ＝４だから、ＡＯ＝２ｃｍ
正四角錘ＡｰＢＣＤＥの体積＝底面積×高さ÷３＝８×２÷３＝16/３ｃｍ³
ウ…16/３　（21.4％！）

続いて、展開図問題。

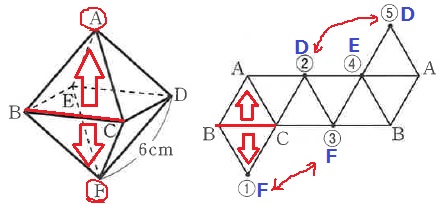
アプローチはいろいろある。
たとえば、ＢＣに着目して、辺ＢＣを共有する正三角形は△ＡＢＣと△ＢＣＦ。
△ＡＢＣでＢＣの反対側はＡ、△ＢＣＦでＢＣの反対側はＦ。
Ａはすでに記されているので、もう片方の①はＦとなる。
このように１つずつ調べていく。

展開の仕方から、①と③が重なるので、③もＦとなる。
同様に、②と⑤も重なる。

また、正八面体において、頂点ＣからＡＢＤＦは隣同士に位置するが、
ＥだけはＣから離れている。
展開図でいえば、④がＣと隣同士になる可能性がない。
よって、④がＥとなる。　エ…④　（52.7％）

『最も短い』→直線
だいたい三平方を使うので、ＢＥを斜辺とする直角三角形を作成する。

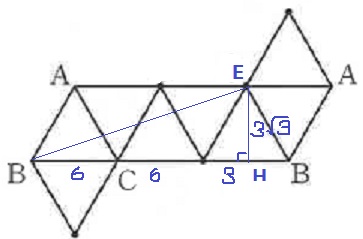
Ｅから垂線をおろし、交点をＨとする。
ＥＨは正三角形を縦に２分するので、30°－60°－90°の直角三角形ができる。
１：２：√３より、ＥＨ＝３√３
ＢＨ＝√（15²＋３√３²）＝√252＝６√７ｃｍ
オ…６√７　（12.0％！）

（２）　0.5％!!!
まずは形を確認。

三角錐ＣＰＦＱは、三角形ＰＱＦを底面とすると、高さが一定。
この高さは、正方形ＢＣＤＥの対角線ＥＣの半分→３√２ｃｍ

正八面体の体積は正方形ＡＢＦＤを底面として、６×６×３√２÷３×２＝72√２ｃｍ³
三角錘ＣＰＦＱの体積が、72√２÷６＝12√２ｃｍ³になればいい。

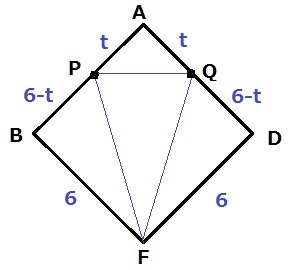
ＡＰ＝ＡＱ＝ｔとおいて、△ＰＦＱの面積をｔで表す。
６×６－ｔ×ｔ×１/２－６×（６－ｔ）×１/２×２
＝－ｔ²/２＋６ｔ

三角錘ＣＰＦＱの体積は、
（－ｔ²/２＋６ｔ）×３√２×１/３＝12√２
（－ｔ²/２＋６ｔ）×√２－12√２　←すべてに√２をかける。
＝２（－ｔ²/２＋６ｔ）－24　←カッコを展開し、すべてに－をかける。
＝ｔ²－12ｔ＋24＝０
因数分解ができないので、解の公式。
ｔ＝（12±４√３）/２＝６±２√３
０≦ｔ≦６（ＰとＱは６秒でＢとＤに到着する）ので、
ｔ＝６－２√３
６－２√３秒後

＠余談＠
もうちょっと良い方法ないかなと思案してみました。

四角錘Ｃ－ＡＢＦＤは、正八面体の半分。
三角錘Ｃ－ＰＦＱが、四角錘Ｃ－ＡＢＦＤの体積の１/３になれば、
正八面体の面積の１/６になる。（正八面体の半分の１/３倍だから）

正方形ＡＢＦＤにおいて、この３分の１の面積が△ＰＦＱになる。
残りの面積が、正方形の３分の２になればいい。
６×６×２/３＝24ｃｍ²　…△ＰＦＱ以外の面積
ｔ×ｔ×１/２＋６×（６－ｔ）÷２×２＝24
ｔ²－12ｔ＋24＝０
解の公式→ｔ＝６－２√３

考え方は先ほどと同じですけど、
正方形ＡＢＦＤにおいて、△ＰＦＱ以外が24ｃｍ²だと早めに決めてしまえば、
計算処理がややショートカットできます。
公立高校入試解説ページに戻る