問題ＰＤＦ
＜図１＞のように、たて３ｃｍ、横６ｃｍの長方形があります。
これを１ｃｍごとに区切ってできる18個のます目に、次の〔ルール〕で色をぬります。
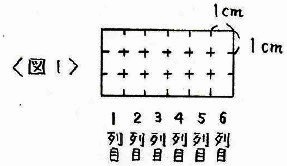
〔ルール〕
・それぞれの列について、３つのます目のうち少なくとも１つはぬる。
・色をぬったます目の真下のます目はすべてぬる。
例えば、＜図２＞の場合、ぬった部分の面積は13ｃｍ2、まわりの長さは20ｃｍとなります。
次の問に答えなさい。
（１）
面積が17ｃｍ2となったとき、まわりの長さとして考えられる長さをすべて求めなさい。
（２）面積が15ｃｍ2となったとき、
（ア）
まわりの長さとして考えられる長さをすべて求めなさい。
（イ）
まわりの長さが最も長くなるようなぬり方は何通りありますか。
（３）まわりの長さが最も長くなったとき、
（ア）
面積が最も大きくなる場合と最も小さくなる場合との例を１つずつ、
下のます目にぬりなさい。
（イ）
ます目のぬり方は（ア）の２通りもふくめて、全部で何通りありますか。
＠解説＠
（１）
面積が17ｃｍ2ということは、１マス塗られない。
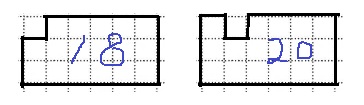
３階の角か中かの２通り。18ｃｍ2、20ｃｍ2
（２）ア
面積が15ｃｍ2→３マス塗られない。
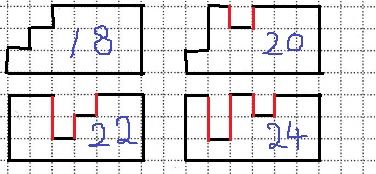
左上の18を基準に、３階のどこかボコ（凹）ができると周りの長さが増える。
赤い線が増えるところ。
よって、18ｃｍ、20ｃｍ、22ｃｍ、24ｃｍ。
イ
周りの長さが最も長くなる形は、２凹と１凹の形。
２凹と１凹は２～５列目の中で、かつ隣り合ってはいけない。
〔２列目－４列目〕〔２列目－５列目〕〔３列目－５列目〕の３パターン。
２凹と１凹が反対になる場合もあるので、各々で２通り。
２×３＝６通り
（３）ア
周りの長さを最も長くするには、２凹を２つ作る。
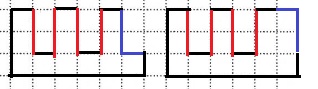
赤いところで長さを稼ぐ。
青いところはどちらでも変わらない。
左が面積最小で、右が面積最大となる。
イ
どこで終わりか確証が得ずらいので不安いっぱいになる。
場合分けの整理としては、３階部分が３つか４つに分ける。
３つの場合は隣り合わせにしない。そうしないと、２凹が２つできない。
↑図を簡略化しました。
Ａが３階が３つパターン。４通り。
Ｂが３階が４つパターン。
隣り合わせになる２列の位置が３通り。
Ｃは形がＢと似ているが、３階が隣り合う場所の２つの角のうち、１つを２階にするパターン。
１マス減らしても周りの長さが変わらない。
各々で２通り。２×３＝６通り
したがって、４＋３＋６＝１３通り
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント