問題PDF
(1)①〔 〕にあてはまる1以上の整数の組は何個ありますか。
11×〔 ア 〕+23×〔 イ 〕=2024
②〔 〕にあてはまる1以上の整数の組を1つ答えなさい。
8×〔 ウ 〕+11×〔 エ 〕+23×〔 オ 〕=2024
(2)
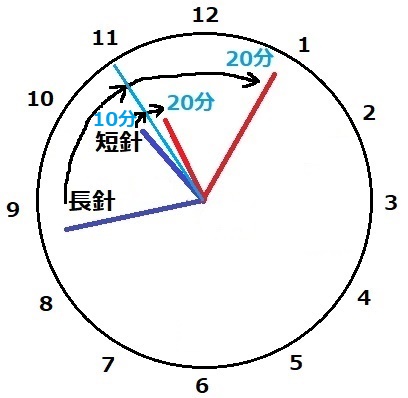
現在、時計の針は10時〔 カ 〕分〔 キ 〕秒を指しています。
長針と短針のつくる角度が現在と20分後で変わらないとき、
〔カ〕〔キ〕にあてはまる数を(カ、キ)の形ですべて答えなさい。
ただし、キの値は分数で答えなさい。
(3)
下の図のような正方形のタイルを並べて模様をつくります。
次の形を並べるとき、何通りの模様が考えられますか。
ただし、タイルは回転して使ってもよいですが、裏面は使いません。
また、回転して同じ模様になるものは1つの模様とみなします。

(4)①
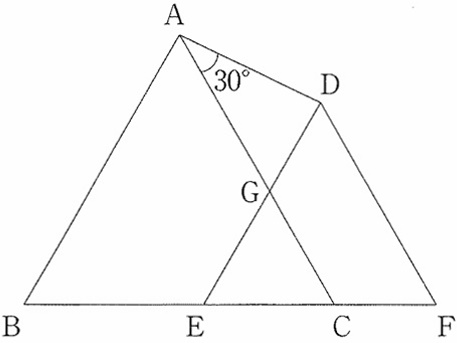
下の図のように、1辺の長さが4cmの正三角形ABCと1辺の長さが3cmの正三角形DEFがあり、辺ACと辺DEが交わる点をGとします。三角形AGDにおいて角Aの大きさが30°のとき、三角形AGDと三角形GECの面積の比を最も簡単な整数の比で表しなさい。
②
1辺の長さが3cmの正三角形と1辺の長さが4cmの正三角形の面積の和は、1辺の長さが5cmの正三角形の面積に等しいことを、①を利用して説明しなさい。
@解説@
(1)①
年度問題。2024=8×11×23
【11×0+23×88=2024】
11と23は互いに素。11×23=23×11で交換できる。
11の個数を+23、23の個数を-11して交換していく。
11×23+23×77
11×46+23×66
11×69+23×55
…
11×□+23×11=2024
1以上の整数だから、23×(11~77)の7個。
②
11か23の個数を減らして8の倍数をつくる。
11×23+23×77=2024→【8×0+11×23+23×77=2024】と付け加え、
前問のように8の個数を+11、11を-8して交換すると、
8×11+11×15+23×77=2024になる。
ウ…11、エ…15、オ…77
@余談@
解答は他にもある。
8と11の交換を再度行うと、8×22+11×7+23×77
8と23を1回交換すると、8×23+11×23+23×69
11×46+23×66など他を基準に交換してもOK。
11の倍数と23の倍数をうまく組み合わせて、8の倍数に変換してもできます。
(2)
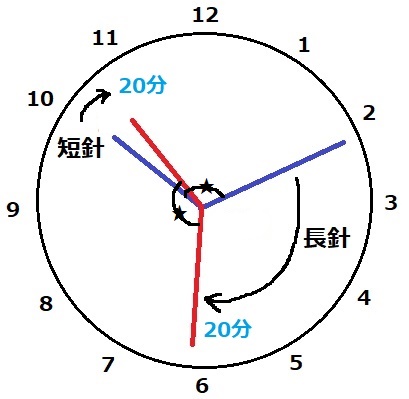
青線の時刻から20分経過すると赤線の時刻になり、あいだの角が等しくなった。
青線の時刻を求めたい。
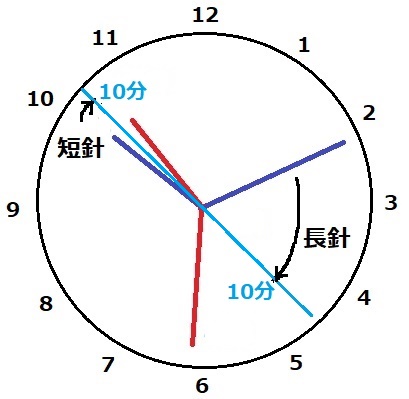
計算がしやすいように、長針と短針が特殊な位置関係になるときを考える。
対称軸を意識すると、青線から10分後に長針と短針が一直線になる。
ということは、青線の時刻は長針と短針が一直線になったときから10分前。
10時では長針と短針は300°離れており、一直線=180°なので、
2つの針の差が300-180=120°縮まればいい。
1分あたり長針6°、短針0.5°、差は5.5°縮まるから、
120÷5.5-10=130/11分=11・9/11分
9/11分=60×9/11=540/11=49・1/11秒
1回目…11分49・1/11秒
2回目は長針が短針を追い越した後に起こる。(11時を過ぎてもOK)
今度の対称軸では長針と短針が一致し、一致から10分前が青線の時刻となる。
10時の300°差が0になる→300÷5.5-10=490/11分=44・6/11分
6/11分=6/11×60=360/11=32・8/11秒
2回目…44分32・8/11秒
(11、49・1/11)(44、32・8/11)
(3)①
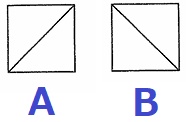
タイルの向きは2種類ある。それぞれをA、Bとする。

Aの枚数で整理。
留意点はAが2枚のとき、配置が2パターンある。
6通り
②
それぞれのマスにAかBのどちらかをいれる。
全体は、2×2×2×2×2=32通り
ここから回転して重複するものを引き、余事象から求める。
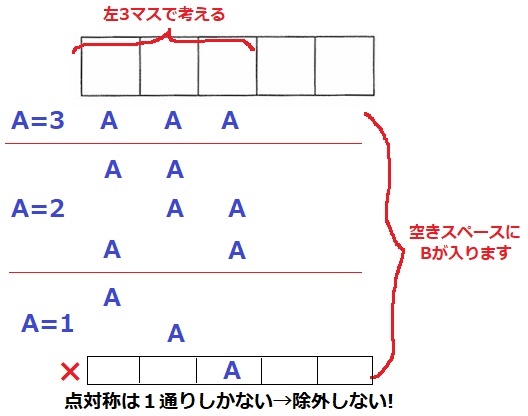
左右逆の並びであれば回転で重複する。左3マスのAの配置で場合分け。
A=3は1通り
(AAABBを回転させたBBAAAを除外する)
A=2は3通り
(BAABBならば、これを回転させたBBAABを除外)
A=1は2通りしかない点に注意する!
BBABBは点対称。点対称は1通りしかなく、重複が発生しない。
1+3+2=6通り
AをBに入れ替えた場合も含めて、除外対象は6×2=12通り
32-12=20通り
@別解@
次の問題では直接数え上げましたが、本問でもできました。
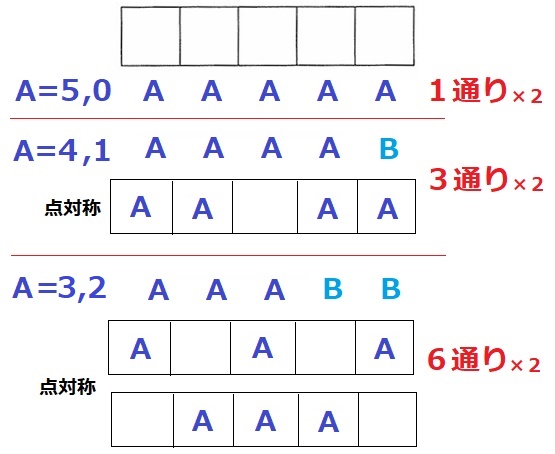
A=5、0のとき、1通りずつ。
A=4、1のとき、Bがどこに入るかで5通り。
点対称は1つ。点対称以外は(5-1)÷2=2通り。点対称を含めて3通りずつ。
A=2、3のとき、5C2=10通り
点対称は2つ。(10-2)÷2+2=6通りずつ
全部で、(1+3+6)×2=20通り
③
Aの枚数で重複パターンを探る。
A=6(すべてA)とA=0(すべてB)は1通りずつ。
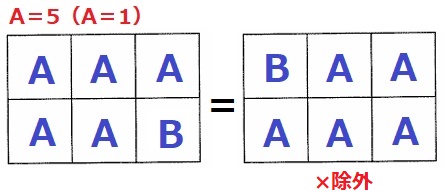
A=5枚のとき、配置は6C5=6C1=6通り
このうち、半分は回転させると重複するので6÷2=3通り
A=1枚のときも対称性から3通り。

A=4枚のとき。全体は6C4=6C2=15通り
前問のように、点対称の配置では1通りしかなく、除外対象ではない!
点対称は3通りある。
(15-3)÷2=6通り
点対称を含めて、6+3=9通り
A=2枚も同様に9通り。
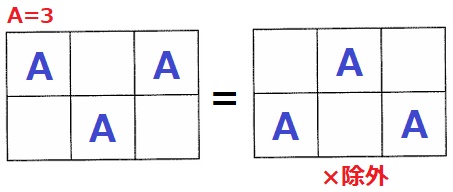
全体は、6C3=20通り
点対称はなく、20÷2=10通り
したがって、(1+3+9)×2+10=36通り
(4)①
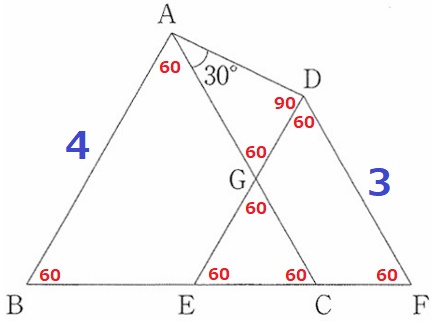
△ABCと△DEFは正三角形。
長さがわかりにくいので、とりあえず角度を記していく。
意味深な30°を含む△AGDの内角は30°―60°―90°

正三角形の辺から別の場所に長さを切り替えたい。
ここでACとDFが平行であることに着目する。
FDを延長し、Aを通るBFに平行な線との交点をHとする。
四角形ACFHは平行四辺形で、HD=4-3=1cm
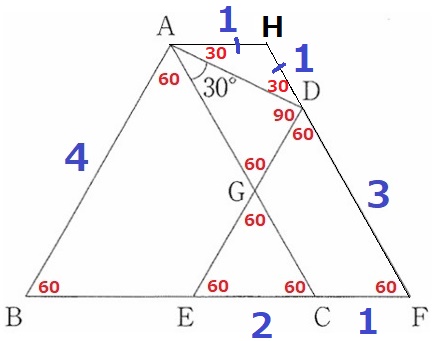
△ADHの内角を調べると底角が30°で等しい二等辺三角形。
AH=1cm
AH=CF=1cm、EC=3-1=2cm
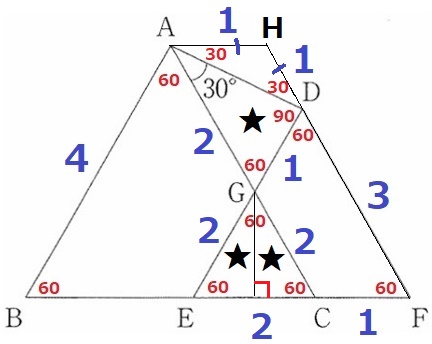
正三角形の辺を頼りに長さを書いていくと、
上図はなんか変ですが、★は合同な直角三角形である。
△AGD:△GEC=1:2
②
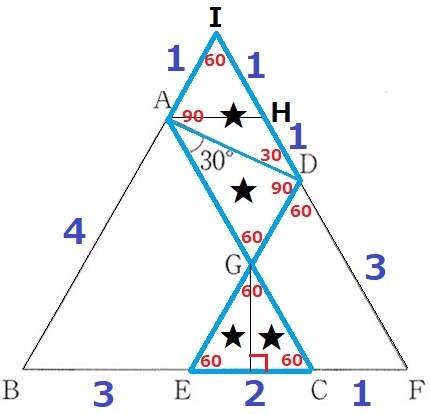
BAとFDを延長した交点をIとすると、△IBFは1辺5cmの正三角形である。
△ABC+△DEFが重複する△GECの面積が四角形IAGDに相当すると示せばいい。
四角形IAGDは2組の対辺が平行だから平行四辺形。
その対角線ADは平行四辺形を2等分するので、△ADI=★
△GEC=四角形IAGD=★★だから、
1辺3cmの正三角形+1辺4cmの正三角形=1辺5cmの正三角形となる。



コメント