2024年度　久留米大学附設中学過去問【算数】大問４解説

問題ＰＤＦ
図１は、１辺の長さが３ｃｍの正方形です。図２は、図１の正方形を６枚はり合わせた立方体の中にある正四面体です。図３はある立体の展開図で、正方形１つ、正三角形２つ、台形２つからできています。図１から図３の〇は、すべて同じ長さを表しています。


（１）
図３の正方形ＡＢＣＤの面積は何ｃｍ²ですか。

（２）
図２の正四面体の体積は何ｃｍ³ですか。

（３）
図３で点Ｇは辺ＥＦの真ん中の点で、点Ｈは正方形ＡＢＣＤの対角線の交点です。
図３の立体を組み立てたとき、
（ア）ＧＨの長さは何ｃｍですか。
（イ）この立体の体積は何ｃｍ³ですか。

＠解説＠
（１）

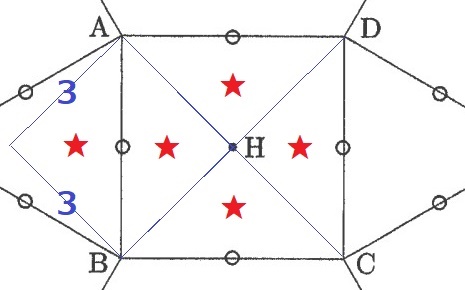
正方形ＡＢＣＤを対角線で４等分（★）すると、１辺３ｃｍの正方形２個分である。
３×３×２＝18ｃｍ²

（２）

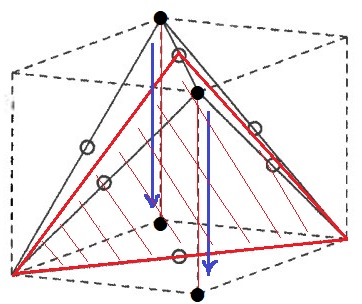
四面体を縦に２等分する赤い三角形は底面に対して垂直で、立方体の高さの辺と平行である。
→等積変形で上の頂点●を底面に移動させると、

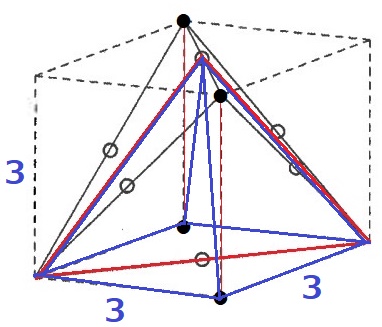
四面体が正四角錐に変形できる。
３×３×３÷３＝９ｃｍ³

（３）ア

立体の描写が難しかった。。組み立てると右図のようになる。

四面体を立体の中にあてはめる。
サイドの正三角形の１辺が〇なので、そこにはめるのが良い。
ＧＨは立体の高さにあたり、四面体が収納された立方体の高さ３ｃｍに相当する。
３ｃｍ

イ

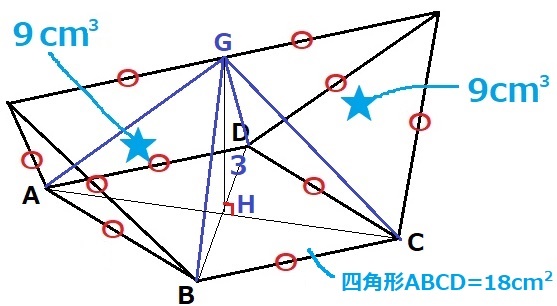
（２）より、四面体★＝９ｃｍ³
（１）より正方形ＡＢＣＤの面積が18ｃｍ²なので、
正四角錐Ｇ―ＡＢＣＤの体積は、18×３÷３＝18ｃｍ³
立体の体積は、９×２＋18＝36ｃｍ³