2024年度　ラ・サール中学過去問【算数】大問５解説

問題ＰＤＦ
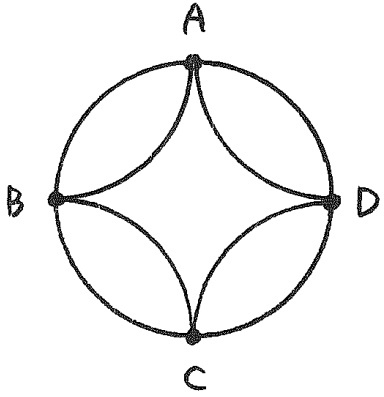
下図のように、４つの地点Ａ、Ｂ、Ｃ、Ｄが道でつながっています。
Ａを出発地点として同じ道を通らないように８つの道すべてを通る道順のうち、
地点間の移動が次のようになる道順は何通りありますか。

（１）
Ａ→Ｂ→Ａではじまる道順

（２）
Ａ→Ｂ→Ｃ→Ｄ→Ａではじまる道順

（３）
Ａを出発地点とするすべての道順

＠解説＠
（１）

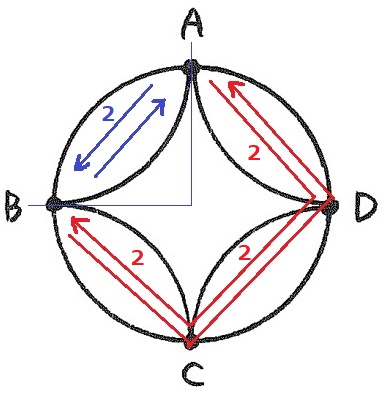
行きが決まると帰りの道も決まるので、Ａ→Ｂ→Ａは２通り。

（２）

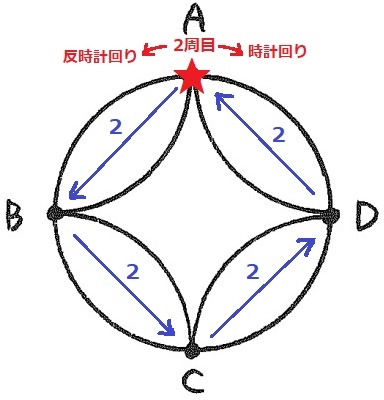
１周目は反時計回りでＡに戻る。２×２×２×２＝16通り
２周目は時計回りか反時計回りしかない。
16×２＝32通り

（３）

Ａから出発して、行きの道を決めると帰りの道は１つしかない。
（１）では青ルートでＢまで行ってＡに戻り、赤ルートでＢまで行って戻って16通りだった。
結局、最後はＡに戻ってくるので、どこで折り返すか、先にどちら回りかで決まる。
折り返し地点がＢのとき、赤ルート→青ルートを含めると、16×２＝32通り

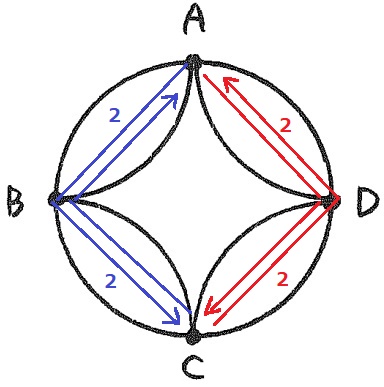
折り返し地点がＣの場合も同様。
２×２×２×２＝16通り、青と赤どちらを先に回るかで16×２＝32通り
Ｄも同様に32通り。

折り返し地点がＡの場合、（２）より１周目で反時計回りして32通りだった。
１周目が時計回りの場合も32通り。
合わせると、32×５＝160通り
難関中（算数科）解説ページに戻る