問題PDF
同じ整数を2回かけてできる数を平方数といいます。
平方数を次のように〇を用いて表すことにします。
例えば、45×45=2025ですから、2025は45の平方数であり、これを2025=㊺と表します。
(1)
〔 〕にあてはまる数を答えなさい。
1から5までの連続する整数の平方数の和①+②+③+④+⑤を、次のような考え方で計算します。
①+②+③+④+⑤
=1×1+2×2+3×3+4×4+5×5
=1+(2+2)+(3+3+3)+(4+4+4+4)+(5+5+5+5+5)
+で結ばれている15個の数を図1のように並べます。これらの数を、120°反時計回りに回転させた位置(図2)と時計回りに回転させた位置(図3)に並べます。
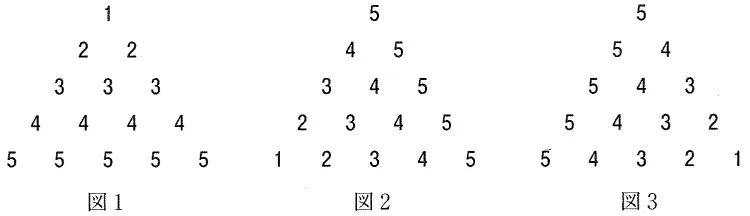
3つの図において、同じ位置にある3個の数をたすと、どの位置でも〔 ア 〕になります。このことを利用して①+②+③+④+⑤を計算すると、〔 イ 〕になります。
同じように考えて、1から11までの連続する整数の平方数の和
①+②+‥‥‥+⑪を計算すると〔 ウ 〕になります。
(2)
2024は2から連続する偶数の平方数の和で表すことができます。
その表し方を、〇を用いて答えなさい。ただし、途中を「‥‥‥」で省略してもかまいません。
(3)
3から連続する3の倍数の平方数の和で表すことができる5けたの整数のうち、
最も大きいものを求めなさい。
@解説@
(1)
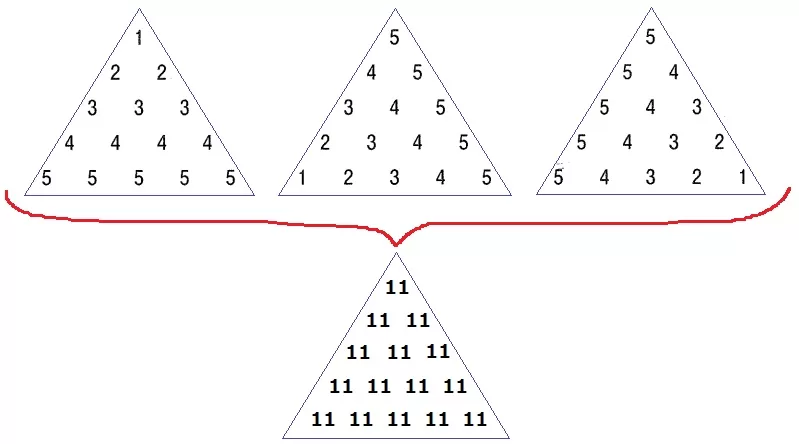
3つの三角形を合わせると、すべて11の三角形になる。
たとえば、上の頂点だと1+5+5=11
3段目の真ん中では、3+4+4=11
11の個数は1~5の和で(1+5)×5÷2=15個
11の三角形は3つの三角形の和、求めたいのは三角形1つ分だから、
11×15÷3=55
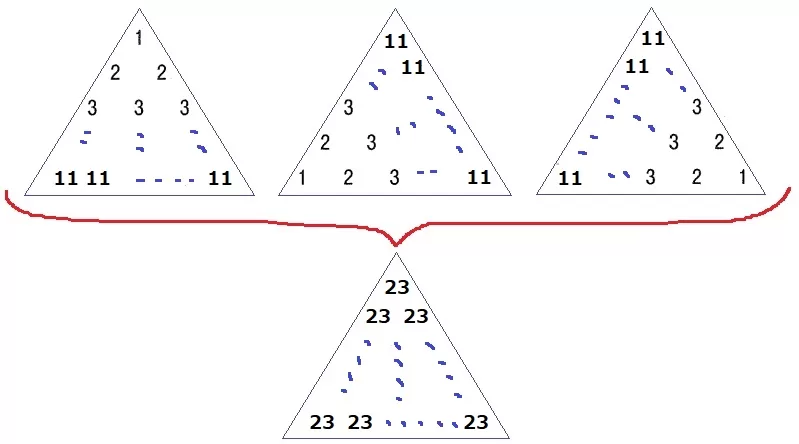
3つの三角形を合わせると、すべて23になる。
23の個数は1~11までの和→(11+1)×11÷2=66個
23×66÷3=506
ア…11、イ…55、ウ…506
(2)
偶数の平方数だけを抜き出す。
(2×2)+(4×4×4×4)+(6×6×6×6×6×6)+…=2024
前問のような三角形をつくることを考える。
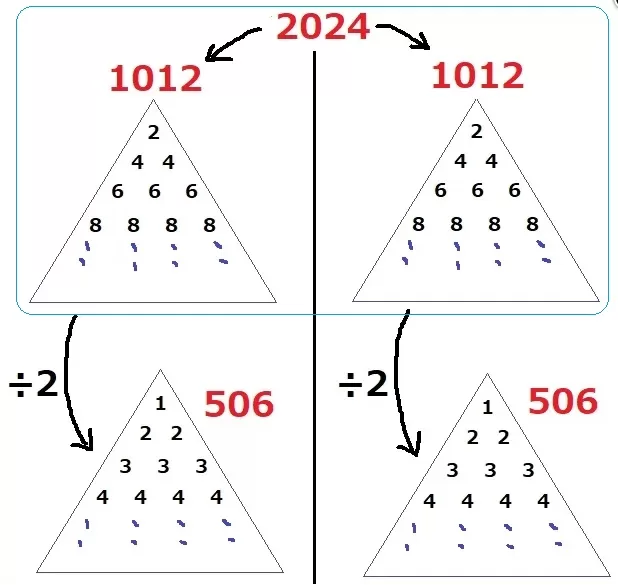
数列の個数を1+2+3+…と三角数に置き換えるために数列を半分に分ける。
(2×2)+(4×4×4×4)+(6×6×6×6×6×6)+…
2×(1×1)+2×(2×2×2×2)+2×(3×3×3×3×3×3)…=2024
さらに÷2すると、(1)の考え方が使える。
三角形の和が506となるのは何段目かを調べればいいが、
先ほど(ウ)で①+②+‥‥+⑪=506だったから11段である。
2倍して戻すと、②+④+‥‥+㉒
(3)
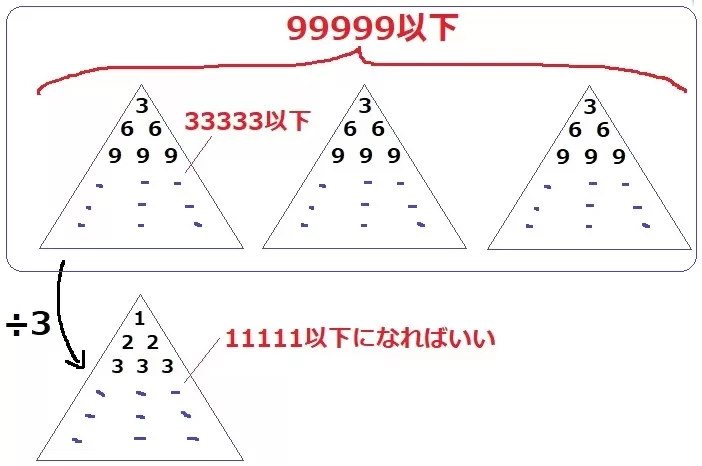
3の倍数なので三角形を3個つくる。
1個の三角形の和が33333以下、これを÷3した三角形の和が11111以下になればいい。
ここからどうするか。。
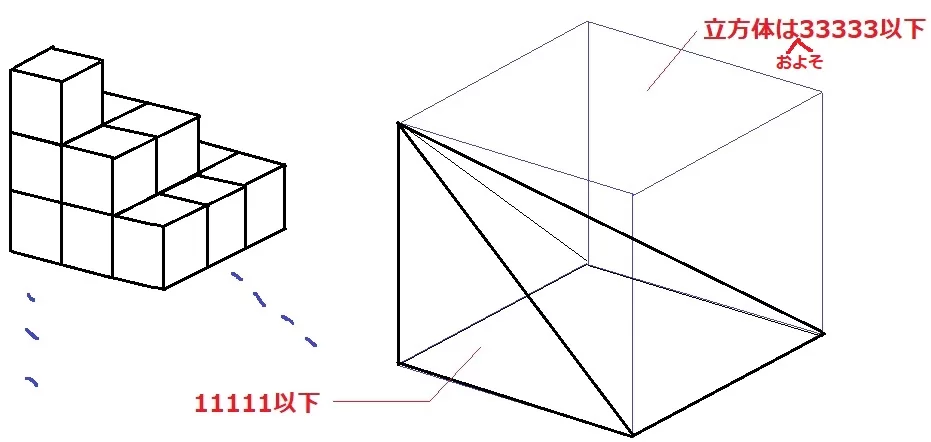
平方数を足していく作業を図形に置き換えてみる。
1段目…1×1、2段目…2×2、3段目…3×3とブロックを積み重ねると全体は四角錐になる。
錐の3倍が柱。すなわち、立方体が約33333以下になればいい。
30×30×30=27000だから30ちょっと上。
試しに32で計算してみると、
(1+32+32)×{(1+32)×32÷2}÷3=11440 ←11111over!
31に下げる。11440-32×32=10416 ←OK!
3倍して3の倍数の三角形に戻し、さらに3倍する。
10416×9=93744



コメント