2019年度　豊島岡女子学園中学過去問３回目【算数】大問６解説

問題ＰＤＦ
底面が正方形である正四角すいＡ－ＢＣＤＥがあり、辺ＡＢ、ＡＣ、ＡＤの真ん中の点をそれぞれＦ、Ｇ、Ｈとします。この正四角すいＡ－ＢＣＤＥを机の上に置き、平面で切り取ったときに残った立体を考えます。
この立体を、上から見た図を正方形のマス目の方眼紙にかきます。例えば３点Ｆ、Ｇ、Ｈを通る平面で切り取ったときに残った立体を上から見ると＜図１＞のようになり、３点Ｆ、Ｇ、Ｄを通る平面で切り取ったときに残った立体を上から見ると＜図２＞のようになります。ただし、図の中の○は底面からの高さが同じ点を表すものとします。

（１）
ＡＦ、ＡＧの真ん中の点をそれぞれＭ、Ｎとし、３点Ｆ、Ｇ、Ｈを通る平面を（あ）、３点Ｍ、Ｎ、Ｄを通る平面を（い）とします。正四角すいＡ－ＢＣＤＥを２つの平面（あ）、（い）で切り取ったときに残った立体を上から見た図として最もふさわしいものを①～④から選びなさい。

（２）
正四角すいＡ－ＢＣＤＥをいくつかの平面で切り取ったときに、残った立体を上から見ると＜図３＞のようになりました。このとき、元の正四角すいＡ－ＢＣＤＥの側面だった部分を＜図４＞の①～⑥の中からすべて選びなさい。

（３）
下の〔　ア　〕、〔　イ　〕に当てはまるものを①～⑨からそれぞれ選びなさい。
「正四角すいＡ－ＢＣＤＥをいくつかの平面で切り取ったときに、残った立体を上から見た図が、＜図５＞のようになることはない。その理由は、〔　ア　〕が同じ平面の上の点ではないからである。なお、＜図５＞で〔　イ　〕が結ばれていると、残った立体を上から見た図になる」

①４点Ｄ、Ｅ、Ｋ、Ｊ　②４点Ｂ、Ｃ、Ｊ、Ｉ　③４点Ｅ、Ｂ、Ｉ、Ｋ
④３点Ｃ、Ｄ、Ｊ　　　⑤３点Ｊ、Ｋ、Ｉ　　　⑥２点Ｅ、Ｉ
⑦２点Ｄ、Ｋ　　　　　⑧２点Ｂ、Ｋ　　　　　⑨２点Ｃ、Ｉ

＠解説＠
（１）

こんな感じで２つの面を切断する。

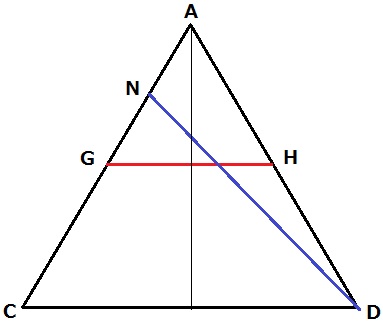
↑面ＡＣＤを正面にみた図。
計算するまでもなく、ＧＨとＮＤの交点はＧＨの中点より右側にくる。
④

（２）

白丸○は同じ高さの点なので、①は底面と平行。
①の三角形の頂点の場所に注目。
正方形の中央と、正方形の中央～辺までの中点に頂点があるということは、
図１のようにＦ、Ｇ、Ｈを通る平面（正四角錘の高さの半分）で切断されたということ。

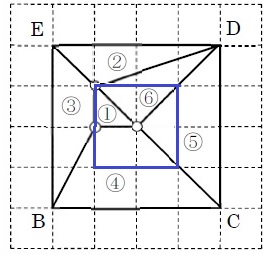
青線のラインが①と同じ高さになるはず。
この内側を侵食する④・⑤・⑥は①の高さの平面からさらにカットしたので、
元の正四角錘の側面ではない。
②、③は白丸から底面の１辺ＥＢ、ＥＤに向けて面が伸びているので、元の正四角錘の側面である。
②、③

（３）

ぱっと見てＢ、Ｃ、Ｊ、Ｉに違和感を覚える。
ＩとＪが同じ高さにあるので、ＩＪからＪ→Ｃ方向に切り込みを入れるとＩ→Ｂ方向にいかない。
これはＩから出発したとき、Ｂの位置がＩＪの平行線よりも手前にあるから。
この矛盾を解消するにはＩＣに線を結ぶ。
ア…②、イ…⑨
難関中（算数科）解説ページに戻る