2023年度　市川中学過去問【算数】大問２解説

問題ＰＤＦ
ある川に上流の地点Ｐと、下流の地点Ｑがあります。
ＰからＱまで川を下るのに、Ａ君は30分かかり、Ｂ君は60分かかります。
Ａ君がＰからＱに向かって、Ｂ君がＱからＰに向かって同時に出発したところ、
25分後に出会いました。このとき、次の問いに答えなさい。

（１）
Ｂ君はＱからＰまで川を上るのに何分かかるか求めなさい。

（２）
Ａ君とＢ君の静水時の速さの比を求めなさい。

（３）
ある日、川の流さの速さが通常時の1.5倍になりました。
このとき、Ａ君がＰからＱに向かって、Ｂ君がＱからＰに向かって同時に出発すると、
２人は何分後に出会うか求めなさい。

＠解説＠
（１）

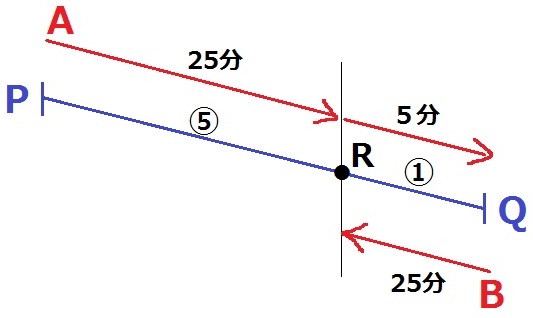
ＡとＢが出会った地点をＲとする。
最初はＡに着目する。
ＡはＰ→Ｑを30分で下るので、残りのＲ→Ｑは５分で下る。
速さ一定より、距離の比は時間の比→ＰＲ：ＲＱ＝25：５＝⑤：①

（２）

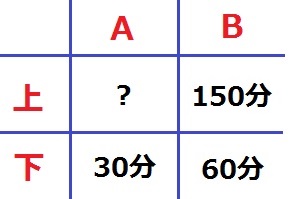
静水時の速さの比を知るには流水の比が必要。
上りと下りの時間が判明しているＢに着目する。

速さの比は時間の逆比。
速さの比は、Ｂ上り：Ｂ下り＝60：150＝②：⑤
Ｂ静水はこの平均で〇3.5。流水＝⑤－〇3.5＝〇1.5

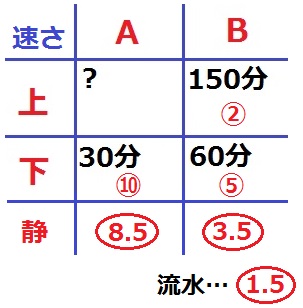
下りの時間の比からＡはＢの２倍の速さなので、
Ａ下り＝⑤×２＝⑩
Ａ静水＝⑩－〇1.5＝〇8.5
Ａ静水：Ｂ静水＝〇8.5：〇3.5＝17：７

（３）

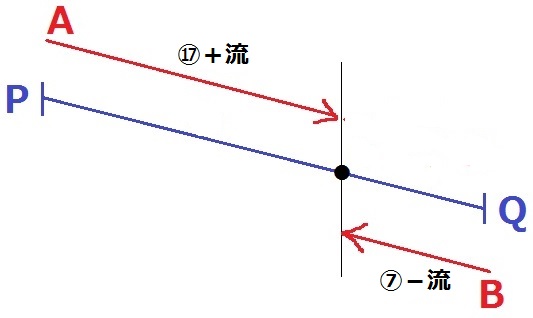
速さの比は、Ａ下り：Ｂ上り＝（⑰＋流）：（⑦－流）
流水の速さが1.5倍でだろうが0.5倍であろうが、
ＡとＢの速さの合計は（⑰＋流）＋（⑦－流）＝㉔で変わらない。
（*流速が変わっても打ち消しあうので、両者が近づく速さは不変である）
速さの合計が一定、ＰＱ間の距離は同じ⇒出会う時間は25分で一定。
25分後
難関中（算数科）解説ページに戻る