問題PDF
(1)
ある文房具店で、ノート3冊のセットを400円、ノート4冊のセットを500円で売ったところ、合計で100冊分のノートが売れ、売り上げは全部で13100円でした。
このとき、ノート3冊のセットは何セット売れましたか。
(2)
2019以下の7の倍数で、2019との差が10の倍数となる数は何個ありますか。
(3)
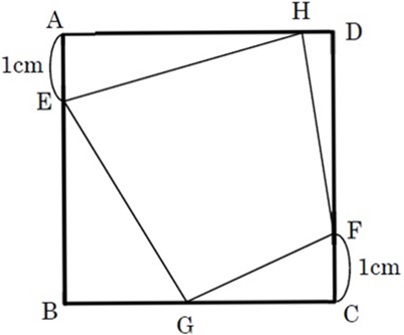
下の図のように、1辺の長さが4cmの正方形ABCDの、辺ABの上に点Eを、辺CDの上に点Fを、AEとCFの長さがそれぞれ1cmになるようにとります。また、辺BCの上に点Gを、辺DAの上に点Hを、BGとDHの長さの和が3cmになるようにとります。このとき、四角形EGFHの面積は何cm2ですか。
(4)
下の図は、三角形ABCの辺ACの真ん中をDとして頂点Bと点Dを結び、頂点Aから辺BCに垂直な直線AHを引いた図形です。角BCAの大きさが30度、角BDAの大きさが45度のとき、角ABDは何度ですか。

@解説@
(1)
3冊セットを○、4冊セットを△とおく。
3×○+4×△=100 …①
400×○+500×△=13100 …②
②-①×125
400×○+500×△=13100
-)375×○+500×△=12500
25×○ =600
○=24
24セット
(2)
『2019と差が10の倍数』⇒一の位は9
はじめの数は、7×7=49
一の位が7であれば、その7の倍数は一の位が9になる。
終わりの数を調査。
2019÷7=288…3 割れない
2009÷7=287 割れた!
7×7、7×17、7×27、7×37・・7×287
【7、17、27、37・・287】←この個数が答えになる。
(287-7)÷10+1=29個
(3)

上のような補助線をひく。
○の合計が3cmなので、なかにできた四角形の横は4-3=1cm
縦は3-1=2cm
外側に4組の合同な直角三角形ができるので、
(全体の正方形+なかの四角形)÷2=四角形EGFHの面積
(4×4+1×2)÷2=9cm2
(4)
角度を調べて図形の特徴をさぐる。

△AHCは30°-60°-90°の直角三角形。
AC=●●とすると、AH=●

HDに補助線をひく。
△AHDの角度はすべて60°⇒正三角形
AH=HD=DA=●
AHとBDの交点をEとする。
∠EDH=60-45=15°
△AEDと△BHEにおいて、
∠EAD+∠EDA=∠EBH+∠EHB
∠EBH=60+45-90=15°
△BHDは、∠HBD=∠HDBとする二等辺三角形。
HB=HD=●
△ABHは直角二等辺三角形。
∠ABD=45-15=30°



コメント