2021年度　穎明館中学過去問【算数】大問４解説

問題ＰＤＦ
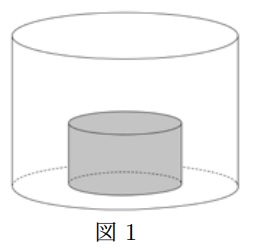
円柱形の水そうの中に、円柱のコンクリートブロックが下の図１のように円の面を下にして置かれています。ブロックの底面の半径と高さは、水そうの底面の半径の１/２です。この水そうに一定の割合で水を注ぎます。このとき、次の問いに答えなさい。

（１）
水を注ぐ時間と水面の高さの関係を表すグラフとして、正しいものはどれでしょうか。

（２）
水を入れ始めてから水そうがいっぱいになるまでに、
水面の高さがブロックと同じになるまでの時間の３倍かかりました。
このとき、ブロックの高さと水そうの深さの比を、最も簡単な整数の比で答えなさい。

（３）
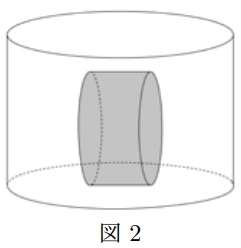
ブロックを下の図２のように置いたとき、
水を注ぐ時間と水面の高さの関係を表すグラフとして、正しいものはどれでしょうか。
（１）の選択肢のなかから答えなさい。

＠解説＠
（１）（２）

（*以下、水面がブロックの高さになるまでを前半、それ以降を後半と記述します）
前半は底面積が小さく、後半は大きくなる。
→水面の高さの変化は前半が急で、後半は緩やか。
水面の高さの変化は１回だけでグラフは湾曲しない。
（１）…ア

ブロックの半径：水槽の半径＝１：２
円の面積比は半径×半径だから、ブロックの底面積を①とすると、
水槽（後半）の底面積は④、前半の底面積は③

『水を入れ始めてから水槽がいっぱいになるまでに、
水面の高さがブロックと同じになるまでの時間の３倍かかった』
水を入れる割合は一定だから、水を入れた時間＝体積比になる。

水面の高さがブロックと同じになる前半の体積を【１】とすると、
水槽の体積は【３】、後半の体積は【２】
高さ＝体積÷底面積

　　　　前半：後半
体積　 【１】：【２】
底面積　　 ③：④       
高さ　　１/３：１/２
＝２：３
前半の高さと水槽全体の高さの比は２：５
（２）…２：５

（３）

底面積の変化をみると、最初は徐々に小さくなっていき、
ブロックの半分を過ぎると再び大きくなっていく。
水面の高さの変化は次第に傾きが急になり、
ある時間から再び緩やかになって、ブロックを過ぎると緩やかな直線となる。

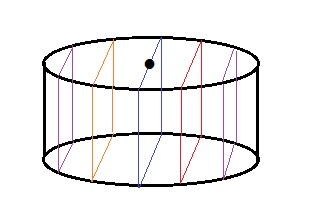
円柱を縦に割ったときの断面積の大きさは常に変化する。
⇒水面がブロックに触れているあいだ、水面の高さの変化率は常に変動する。
グラフは緩やかなＳ字を描く。オ
難関中（算数科）解説ページに戻る