2020年度　久留米大学付設中学過去問【算数】大問５解説

問題ＰＤＦ

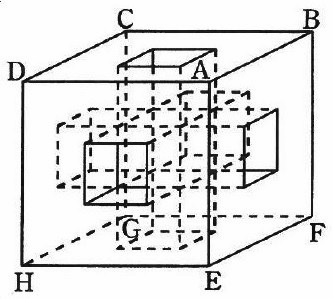
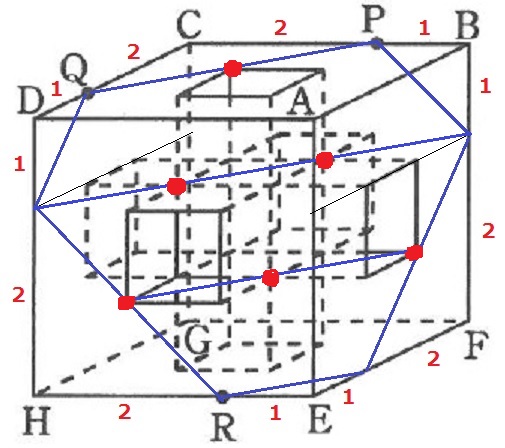
上図のように、一辺の長さが３ｃｍの立方体ＡＢＣＤ－ＥＦＧＨがあり、向かい合った面にある一辺の長さが１ｃｍの正方形を底面とする直方体を３個くり抜きます。底面の正方形は各面の真ん中にあります。そうすると体積が20ｃｍ³の立体ができます。

（１）

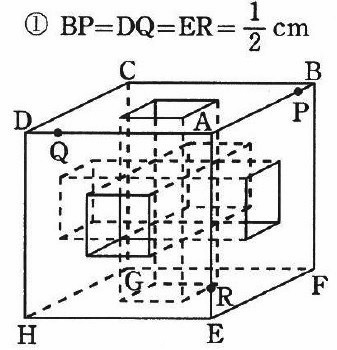
上の①の３点Ｐ、Ｑ、Ｒを通る平面でこの立体を切断します。このとき、切断面の辺の数は何本ですか。また、点Ａを含むほうの立体は四面体Ａ－ＰＱＲから、大きさの同じ四面体を何個引いたものですか。さらに、点Ａを含むほうの立体の体積は何ｃｍ³ですか。

（２）

上の②、③についても同様に、３点Ｐ、Ｑ、Ｒを通る平面でこの立体を切断するとき、点Ａを含むほうの立体の体積はそれぞれ何ｃｍ³ですか。

＠解説＠
（１）

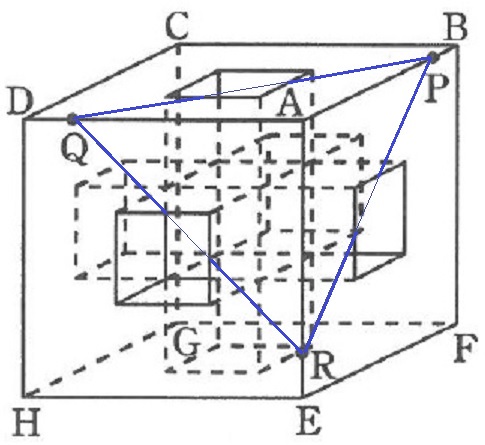
△ＰＱＲは正三角形だけど、中の空洞部分がイジワル(;´Д｀)
高度な空間認識力が試されます。

上からみると45度線なので、これとの平行線に意識する。
ＳＴが見えれば全体像がつかみやすいかと。

問題文に『大きさの同じ四面体』とあるように、空洞部分は３個の合同な四面体。
この１辺の長さを求める。上から見た図で考えよう。
ＤＱ：ＱＡ＝１/２：５/２＝①：⑤
高さに着目して、ＱＳ：ＳＲ（ＳＡ）＝１：３/２＝②：③
ＱＡ＝②＋③＝⑤だから、〇と〇の値は等しい。
ＤＡ＝⑥、ＳＡ＝③だから、ＳはＤＡ(正方形の)１辺の中点。
ここから四面体の横の長さが１/２ｃｍとわかる。
大きな四面体から小さな四面体３つひく。
５/２×５/２×１/２×５/２×１/３－１/２×１/２×１/２×１/２×１/３×３
＝61/24ｃｍ³

＠別解＠
小さな四面体の１辺ですが、もっと簡単に出せました。

立方体の上の面で、正方形の右下の頂点（Ｘ）に触れるように45度線ＵＶを描きます。
（△ＶＡＵは直角二等辺でＶＡ＝ＵＡ＝２ｃｍ）
四角形ＷＱＵＸは２組の対辺が平行な平行四辺形だから、ＷＸ＝ＱＵ＝１/２ｃｍ

（２）②

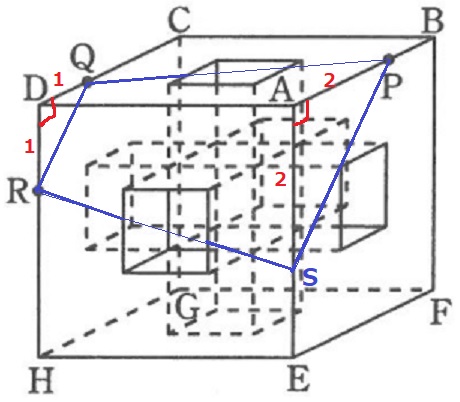
△ＤＱＲが直角二等辺→△ＡＰＳも直角二等辺。
空洞部分はどうなるのか・・。

ＱＲ、ＰＳの45度線を意識して平行線を描く。
赤い角錐台が空洞の部分。青い角錐台は求積する立体に含まれる部分。
角錐台ＤＱＲ－ＡＰＳから赤い角錐台２つを引けばいい。
角錐台ＤＱＲ－ＡＰＳの体積は、２×２×１/２×６×１/３×７/８＝７/２ｃｍ³

問題は赤い角錐台(;´Д｀)
しかし、よく見たら角錐台ＤＱＲ－ＡＰＳと形が似ている。

１辺１ｃｍの正方形２×２の平面【１】と【２】を右側からみた図。
ＤＱ＝③とすると、Ｄからの距離は【１】で④、【２】で⑤、ＤＰ（ＡＰ）＝⑥
直角二等辺の相似図形をアレコレ調べると、直角二等辺の上の辺が①、下の辺が②となり、
角錐台ＤＱＲ－ＡＰＳはＤＱ＝③、ＡＰ＝⑥だから、辺の比が上：下＝１：２で相似！
対応する辺の比は１：３→体積比は１：27
角錐台ＤＱＲ－ＡＰＳの体積を㉗とすると赤い角錐台は①。
求める図形の体積は㉗－①×２＝㉕
したがって、７/２×25/27＝175/24ｃｍ³

③
試験時間内では厳しい。

解説が辛くなってきたので少々省きます。
△ＣＰＱが直角二等辺で、45度線の平行線を描くと上のような感じ。
（１）のように上からみた図で相似を調べると、空洞部分の立方体の頂点●を通過する！

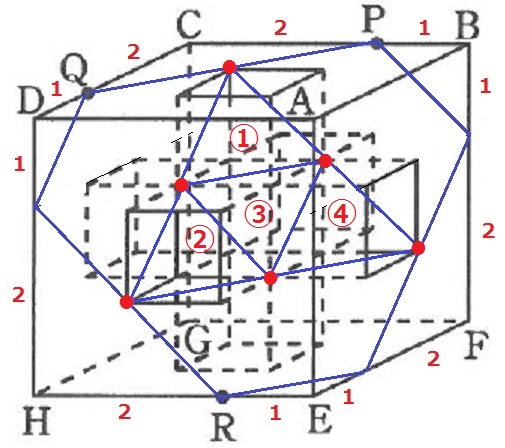
図形がフクザツ過ぎてアウトラインを描けません！
①②④の空洞は１辺１ｃｍの立方体から三角錐を除いた感じ。③の空洞は三角錐です。

どこかの面から相似を捉えると、ＡＸ＝ＡＹ＝ＡＸ＝４ｃｍとなります。
三角錐Ｚ－ＸＹＡから隅の三角錐をひき、１辺１ｃｍの立方体から三角錐を取り除いた立体を３つ分をひき、さらに三角錐をひけば求められます。
４×４×１/２×４×１/３－１×１×１/２×１×１/３×３－（１×１×１－１×１×１/２×１×１/３）×３－１×１×１/２×１×１/３
＝64/６－３/64－３＋３/64－１/64＝45/６＝15/２ｃｍ³
難関中（算数科）解説ページに戻る