問題ＰＤＦ
下の図において、四角形ＡＢＣＤ、四角形ＢＥＦＣ、四角形ＡＥＦＤはすべて平行四辺形です。
ＣＰ：ＰＤ＝６：７、ＰＱ：ＱＥ＝２：１、三角形ＣＱＰの面積が36ｃｍ2のとき、次を求めなさい。
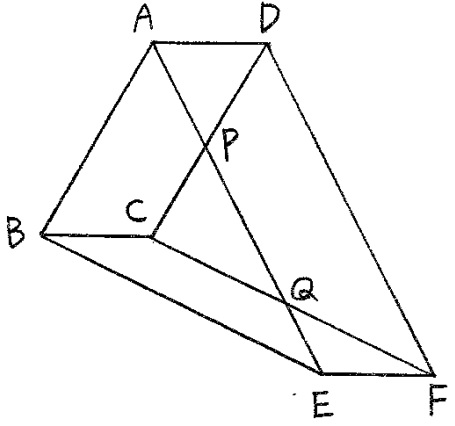
（１）三角形ＱＥＦの面積
（２）三角形ＡＰＤの面積
（３）五角形ＡＢＥＦＤの面積
＠解説＠
（１）
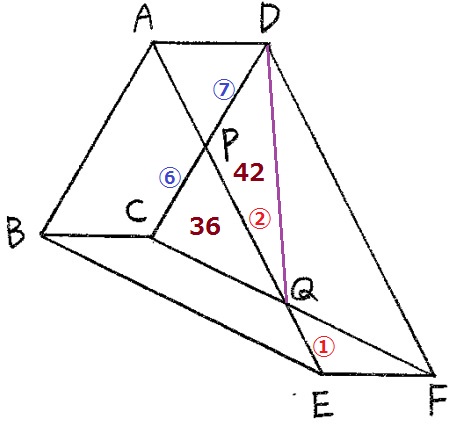
与えられた辺の比から、新たにわかる面積比を探す。
ＤＱに補助線。
ＣＰ：ＰＤ＝△ＣＱＰ：△ＰＱＤ＝⑥：⑦
△ＰＱＤ＝36×⑦/⑥＝42ｃｍ2
ＡＥとＤＦは平行。
△ＰＱＤと△ＱＥＦの高さは等しいので、面積比は底辺の比ＰＱ：ＱＥ＝②：①。
△ＱＥＦ＝42×①/②＝21ｃｍ2
（２）
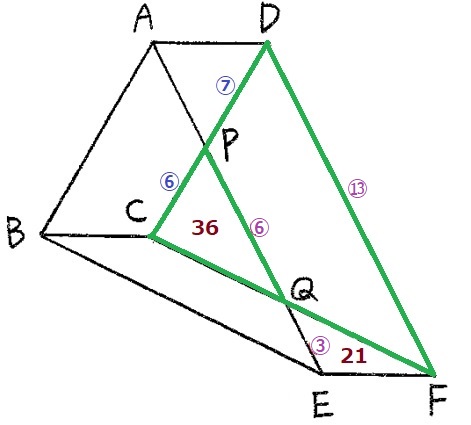
ＰＱとＤＦが平行→△ＣＱＰと△ＣＦＤは相似。
ＰＱ：ＤＦ＝⑥：⑬
ＱＥ＝⑥÷２＝③
平行四辺形の対辺は等しいから、ＡＥ＝⑬
ＡＰ＝⑬－（⑥＋③）＝④
△ＱＥＦ：△ＡＰＤ＝ＱＥ：ＡＰ＝③：④なので、
△ＡＰＤの面積は、21×④/③＝28ｃｍ2
（３）
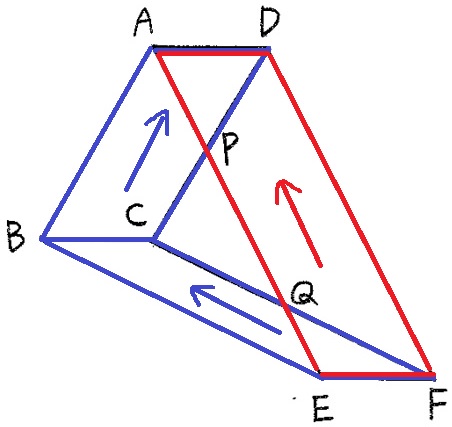
線分ＥＦを赤線方向に平行移動させると、その軌跡は平行四辺形ＡＥＦＤ、
同じ高さの分だけ青線方向に平行移動させると平行四辺形ＡＢＣＤとＢＥＦＣになる。
くの字に曲がった青線を左から押し込むと赤線になり、両者の面積は等しい。
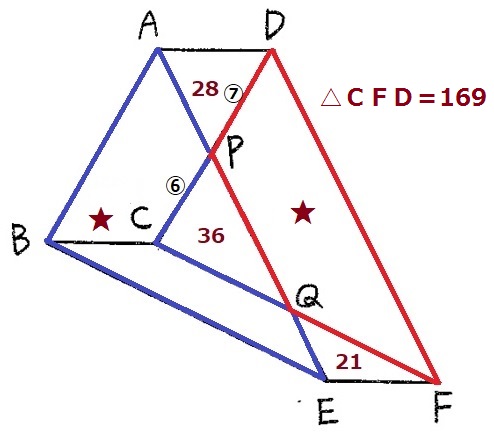
ということは、重複する△ＡＰＤと△ＱＥＦを除外した部分、
すなわち、上図の青線エリアと赤線エリアは等積である。（★）
前問で使った△ＣＱＰと△ＣＦＤの相似に着目すると、
面積比は△ＣＱＰ：△ＣＦＤ＝⑥×⑥：⑬×⑬＝【36】：【169】
ちょうど△ＣＱＰ＝36ｃｍ2なので、△ＣＦＤ＝169ｃｍ2である。
★＝169－36＝133ｃｍ2
五角形ＡＢＥＦＤの面積は、133×２＋28＋36＋21＝351ｃｍ2
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
コメント