問題ＰＤＦ
ある数Ａ以下でもっとも大きい整数を〔Ａ〕と表すことにします。
たとえば、
などのようになります。
（１）
の値はいくつですか。
（２）
の値はいくつですか。
（３） 
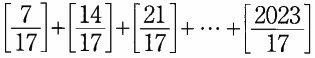の値はいくつですか。
＠解説＠
（１）
はじめはとっかかりを見つけるためにやるしかない(;`ω´)
119までの７の倍数を並べ、あいだに17の倍数をはさむ。
０＋０＋１＋１＋２＋２＋２＋３＋３＋４＋４＋４＋５＋５＋６＋６＋７＝55
＠別解＠
仮分数を帯分数に直したときの分子を調べる。
⑦、⑭、21－17＝④、28－17＝⑪、35－34＝①…と書いていくと、
①～⑯が全部そろっている。これは偶然かしら？(;’∀’)
４と５で試しても同様である。
４と５は互いに素で、４の５番目（20）までを÷５した余りは０～４、
５の４番目（20）までを÷４した余りは０～３で数字がすべてそろっている。。
互いに素であると、最小公倍数（余り０になる数）に到達するまでに、
（順番はきれいでなくても）すべての余りが循環小数のごとく周期的に登場する。
７と17であれば、７の倍数の17番目、17の倍数の７番目に最小公倍数119が登場する。
それまでは必ず余りが発生して、うまい具合に重複を避けながら119で共に１周期を迎える。
そして、ガウス記号は帯分数の分数部分を排除する。
〔21/17〕＝〔１＋４/17〕＝１➡ガウス記号を外すと、21/17－４/17＝１で計算できる。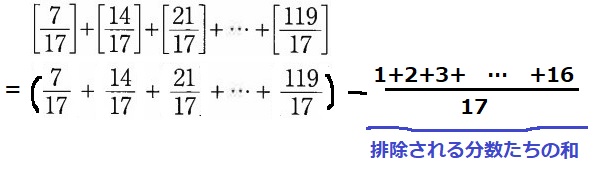
ガウス記号を外した７/17～119/17までの和から、あとで排除される分数の和をひけばいい。
階差数列の和の公式を用いて、
（７＋14＋…＋119）÷17－（１＋２＋…＋16）÷17
＝126×17÷２÷17－17×16÷２÷17
＝63－８＝55
（２）
分子が126から始まり、238で終わる。
119＋７＝126、119×２＝238
（１）の17個の項を１グループ目とすると、（２）は２グループ目にあたる。
排除される分数の分子は前問と同じ⑦、⑭、④、⑪…なので、分数の和は８。
（126＋133＋…238）÷17－８
＝364×17÷２÷17－８
＝182－８＝174
（３）
年度問題。【2023＝７×17×17】
（１）１グループ目は分子７～119（７×17×１）で項が17個。
（２）２グループ目は分子126～238（７×17×２）で項が17個。
17個の項でまとめると、分子2023は2023÷７÷17＝17グループ目のラストの項である。
１グループで排除される分数の和は８で固定。17グループ全体の和は17×８。
すべての項の数は、2023÷７＝17×17＝289個なので、
（７＋14＋21＋…＋2023）÷17－17×８
＝2030×289÷２÷17－17×８
＝1007×17
＝17119
難関中（算数科）解説ページに戻る
国私立高校入試…数学科のみ。ハイレベルな問題をそろえてみました。
難関中算数科…中学受験の要。数学とは異次元の恐ろしさ(;´Д｀)
難関中社会科…年度別。暗記だけじゃ無理な問題がいっぱい！
難関中理科…物化生地の分野別。初見の問題を現場思考でこなせるか。
難問特色検査…英国数理社の教科横断型思考問題。
センター試験…今のところ公民科だけ(^-^;ニュース記事だけじゃ解けないよ！
勉強方法の紹介…いろいろ雑記φ(・・。)
ＱＵＩＺ…☆４以上はムズいよ！
ｎｏｔｅも書いています(っ´ω`c)
入試問題を題材にした読み物や個人的なことを綴っていこうと思います。
気軽にお立ち寄り下さい(*^^*)→サボのｎｏｔｅ
サボのツイッターはコチラ→
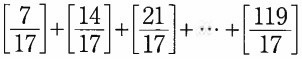
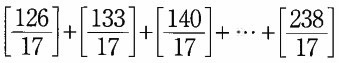
コメント