問題PDF
下の表はかけ算の計算結果を順に並べている表です。上から1段目(つまり一番上の段)、左から2列目のマスには1×2の計算結果(つまり2)が書かれており、上から4段目、左から6列目のマスには4×6の計算結果(つまり24)が書かれています。
紙面の都合上、たても横も15段目、15列目までしか書かれていませんが、「・・・」は、それより先も同じように数が続いていることを表しています。例えば、上から20列目、左から19列目のマスなども、この表には書かれていませんが、あるものとします。

この表をもとにして次の問いに答えなさい。
(問1)
上から5段目、左から8列目のマスに書かれている数から、
上から4段目、左から8列目のマスに書かれている数をひいた数を答えなさい。
(問2)
上から17段目、左から12列目のマスに書かれている数から、
上から16段目、左から12列目のマスに書かれている数をひいた数を答えなさい。
(問3)
上から256段目、左から36列目のマスに書かれている数は、9216でした。
このマスの上にあるマスに書かれている数を答えなさい。
(問4)
上から123456段目、左から654321列目のマスに書かれている数は、そのマスの右上にあるマスに書かれている数に比べて、どれだけ差があるか答えなさい。なお、解答らんの〔 〕には数字を、「 」の中には「大きい」か「小さい」のどちらかを記入しなさい。
@解答欄@
上から123456段目、左から654321列目のマスに書かれている数の方が、
〔 〕だけ、「 」。
(問5)
あるマスに書かれている数と、そのマスの右上にあるマスに書かれている数が同じになることがあります。例えば上から4段目、左から3列目のマスに書かれている数と上から3段目、左から4列目に書かれている数はどちらも12で同じです。それは、「元のマス」の「列の数」、「段の数」がどのようなときですか。「元のマス」、「列の数」、「段の数」を使って説明しなさい。なお、「列の数」とは「左から何列目にあるか」を、「段の数」とは「上から何段目にあるか」を表す数のことです。
@解説@
(問1)
5×8-4×8=8
(問2)
17×12-16×12
=(17-16)×12
=12
(問3)
上から255段目、左から36列目のマスが正解。
255×36…をしてもよいが、問1と問2のように左から〇列目は〇ごとに増えていく。
8列目は8、12列目は12、36列目は36ずつの等差数列。
256×36=9216だから、9216-36=9180
(問4)
ここで差がつく。
123456×654321は計算しない。

左から654321列目なので、1個上にいくと-654321。
上から123455段目なので、1個右にいくと+123455。
654321-123455=530866
〔530866〕だけ「大きい」。
(問5)
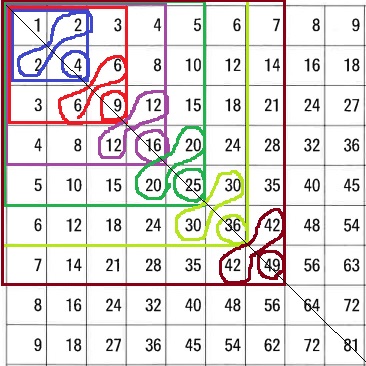
右上と数が同じペアを観察すると見えてくる。
平方数を通るように斜め45度線を描くと右上と左下が対称。
問題文の「元のマス」の意味がよくわからなかったのだが…(;´・ω・)
『あるマス』が元のマスとして、『元のマスの列の数と段の数の差が1のとき』かな?



コメント